Pamoka "Funkcijos y = tgx, y = ctgx, jų savybės ir grafikai". Pamoka "Funkcijos y = tgx, y = ctgx, jų savybės ir grafikai" Funkcijų su liestine tyrimas
Šiame vaizdo įraše aptariamos funkcijų savybės y =tgx, y = ctgx, parodyta, kaip sudaryti jų grafikus.
Vaizdo įrašo pamoka prasideda nuo funkcijos peržiūros y =tgx.
Paryškintos funkcijos savybės.
1) Funkcijos sritis y =tgx vadinami visi tikrieji skaičiai, išskyrus x =π/2 + 2 πk. Tie. grafike nėra taškų, priklausančių linijai x =π/2 ir x = -π/2, taip pat x = 3π/2 ir taip toliau (su tokiu pat periodiškumu). Taigi funkcijos grafikas y =tgx sudarys iš begalinio skaičiaus šakų, kurios bus išdėstytos tarpuose tarp tiesių x = - 3π/2 ir x = -π/2 , x = -π/2 ir x = π/2 ir pan.
2) Funkcija y =tgx yra periodinis, kur pagrindinis periodas yra π. Tai patvirtina lygybę tg(x- π ) = tg x =tg(x+π ) . Šios lygybės buvo tiriamos anksčiau, autorė kviečia studentus jas prisiminti, nurodydama, kad bet kokiai pagrįstai vertei t galioja lygybės:
tg(t+ π ) = tg t ir c tg(t+π ) = ctg t. Šių lygybių pasekmė yra ta, kad jei viena funkcijos y grafiko šaka = tan x tarp eilučių X = - π/2 ir X= π/2, tada likusias šakas galima gauti paslinkus šią šaką išilgai x ašies π, 2π ir pan.
3) Funkcija y =tgx yra keista, nes . tg(- x) =- tg x.
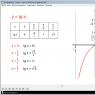
Toliau pereikime prie funkcijos grafiko sudarymo y =tgx. Kaip matyti iš aukščiau aprašytos funkcijos savybių, funkcija y =tgx periodinis ir nelyginis. Todėl užtenka sukonstruoti dalį grafiko – vieną šaką viename intervale, o tada perkėlimui naudoti simetriją. Autorius pateikia lentelę, kurioje skaičiuojamos reikšmės tgx tam tikromis vertėmis x tikslesniam braižymui. Šie taškai pažymėti koordinačių ašyje ir sujungti lygia linija. Nes Jei grafikas yra simetriškas koordinačių pradžios atžvilgiu, tai ta pati atšaka sudaroma, simetriška koordinačių pradžios atžvilgiu. Dėl to gauname vieną grafiko šaką y =tgx. Tada, naudojant poslinkį išilgai x ašies π, 2 π ir tt, gaunamas grafikas y =tgx.
Funkcijos grafikas y =tgx vadinamas tangentoide, o trys paveiksle pavaizduotos grafiko šakos yra pagrindinės tangentoido šakos.
4) Funkcija y =tgx kiekvienu iš intervalų (- + ; +) didėja.
5) Funkcijų grafikas y =tgx nėra jokių apribojimų aukščiau ir žemiau.
6) Funkcija y =tgx neturi didžiausios ir mažiausios vertės.
7) Funkcija y =tgx nuolatinis bet kuriuo intervalu (- - π/2+π;π/2+π). Tiesė π/2+π vadinama funkcijos grafiko asimptote y =tgx, nes šiuose taškuose funkcijos grafikas nutrūksta.
8) Funkcijų reikšmių rinkinys y =tgx vadinami visi realieji skaičiai.
Toliau vaizdo pamokoje pateikiamas pavyzdys: išspręskite lygtį su tgx. Norėdami išspręsti, sukonstruosime 2 funkcijos grafikus adresu ir raskite šių grafikų susikirtimo taškus: tai begalinė taškų rinkinys, kurių abscisės skiriasi πk. Šios lygties šaknis bus X= π/6 +πk.
Apsvarstykite funkcijos grafiką y =ctgx. Funkciją galima pavaizduoti dviem būdais.
Pirmasis metodas apima grafiko sudarymą, panašų į grafiko sudarymą funkcijos y =tgx. Sukurkime vieną funkcijos grafiko šaką y = ctgx tarp eilučių X= 0u X= π. Tada, naudodami simetriją ir periodiškumą, sukonstruosime kitas grafiko šakas.
Antrasis metodas yra paprastesnis. Funkcijos grafikas y = сtgx galima gauti pakeitus liestines naudojant redukcijos formulę Sutgx = - tg(x +π/2). Norėdami tai padaryti, perkelkime vieną funkcijos grafiko šaką y = tgx išilgai x ašies π/2 į dešinę. Likusios šakos gaunamos paslinkus šią šaką išilgai x ašies π, 2π ir pan. Funkcijos y = ctg grafikas x dar vadinama tangentoide, o grafiko atšaka intervale (0;π) yra pagrindinė tangentoido šaka.
TEKSTO IŠKODAVIMAS:
Išnagrinėsime funkcijos y = tan x (y lygus liestinės x), y = ctg x (y lygus kotangentui x) savybes ir sudarysime jų grafikus. Apsvarstykite funkciją y = tgx

Prieš braižydami funkciją y = tan x, užsirašykime šios funkcijos savybes.
SAVYBĖ 1. Funkcijos y = tan x apibrėžimo sritis yra visi realieji skaičiai, išskyrus skaičius, kurių forma yra x = + πk (x lygus pi per du ir pi ka sumai).
Tai reiškia, kad šios funkcijos grafike nėra taškų, priklausančių tiesei x = (gausime, jei k = 0 ka lygus nuliui) ir tiesei x = (x lygus minus pi iš dviejų) (mes gauti, jei k = - 1 ka yra lygus minus vienetui), o tiesė x = (x yra lygi trims pi iš dviejų) (gauname, jei k = 1 yra lygus vienetui) ir tt Tai reiškia, kad grafikas funkcijos y = tan x sudarys iš begalinio skaičiaus šakų, kurios bus išdėstytos intervaluose tarp tiesių. Būtent juostoje tarp x = ir x =-; juostelėje x = - ir x = ; juostelėje x = ir x = ir taip toliau iki begalybės.
SAVYBĖ 2. Funkcija y = tan x yra periodinė su pagrindiniu periodu π. (Kadangi dviguba lygybė yra tiesa
tan(x- π) = tanx = tan (x+π) x atėmus pi liestinė yra lygi x ir lygi x plius pi liestinė). Mes atsižvelgėme į šią lygybę tirdami tangentą ir kotangentą. Priminkime jam:
Bet kuriai leistinai t vertei galioja lygybės:
tg (t + π) = tgt
ctg (t + π) = ctgt
Iš šios lygybės išplaukia, kad sukūrę funkcijos y = tan x grafiko atšaką intervale iš x = - ir x =, likusias šakas gauname perkeldami pastatytą šaką išilgai X ašies π, 2π. , ir taip toliau.
3 SAVYBĖ. Funkcija y = tan x yra nelyginė funkcija, nes lygybė tg (- x) = - tan x yra teisinga.
Nubraižykime funkciją y = tan x
Kadangi ši funkcija yra periodinė, susideda iš begalinio skaičiaus šakų (juostoje tarp x = ir x =, taip pat juostoje tarp x = ir x = ir tt) ir nelyginių, sudarysime dalį grafiką taškas po taško intervale nuo nulio iki pi po du (), tada naudokite pradžios ir periodiškumo simetriją.
Sukurkime braižymo liestinių verčių lentelę.
Randame pirmąjį tašką: žinant, kad esant x = 0 tan x = 0 (x lygus nuliui, tan x taip pat lygus nuliui); kitas taškas: ties x = tan x = (x lygus pi iš šešių, liestinė x lygi šaknims iš trijų iš trijų); Atkreipkime dėmesį į šiuos taškus: ties x = tan x = 1 (x lygus pi iš keturių tan x yra lygus vienetui), o esant x = tg x = (x lygus pi iš trijų tan x yra lygus kvadratinei šaknei iš trijų). Koordinačių plokštumoje pažymėkite gautus taškus ir sujunkite juos lygia linija (2 pav.).
Kadangi funkcijos grafikas yra simetriškas koordinačių pradžios atžvilgiu, tą pačią šaką sudarysime simetriškai koordinačių pradžios atžvilgiu. (3 pav.).
Ir galiausiai, taikant periodiškumą, gauname funkcijos y = tan x grafiką.
Juostoje iš x = - ir x = sukonstravome funkcijos y = tan x grafiko atšaką. Likusias šakas statome perkeldami sukonstruotą atšaką išilgai X ašies π, 2π ir pan.

Sukurtas siužetas vadinamas tangentoidu.
3 paveiksle parodyta tangentoido dalis vadinama pagrindine tangentoido atšaka.
Remdamiesi grafiku, užrašysime dar keletą šios funkcijos savybių.
4 SAVYBĖ. Funkcija y = tan x didėja kiekviename intervale (nuo minus pi dviem plius pi ka iki pi dviem plius pi ka).
SAVYBĖ 5. Funkcija y = tan x nėra apribota nei aukščiau, nei žemiau.
SAVYBĖ 6. Funkcija y = tan x neturi nei didžiausių, nei mažiausių reikšmių.
SAVYBĖ 7. Funkcija y = tan x yra ištisinė bet kuriame formos intervale (nuo minus pi du plius pi ka iki pi du plius pi ka).
Tiesė, kurios forma x = + πk (x yra lygi pi per du ir pi ka sumai) yra vertikali funkcijos grafiko asimptotė, nes x = + πk formos taškuose funkcija patiria nenutrūkstamumas.
SAVYBĖ 8. Funkcijos y = tan x reikšmių rinkinys yra visi tikrieji skaičiai, tai yra (e nuo eff yra lygus intervalui nuo minus begalybės iki plius begalybės).
PAVYZDYS 1. Išspręskite lygtį tg x = (liestinė x lygi šaknei iš trijų iš trijų).
Sprendimas. Sukurkime funkcijų y = tan x grafikus vienoje koordinačių sistemoje
(y yra lygus x liestinei) ir y = (y yra lygus trijų šaknei, padalytai iš trijų).
Gavome be galo daug susikirtimo taškų, kurių abscisės viena nuo kitos skiriasi πk (pi ka) Kadangi tg x = ties x =, tai pagrindinės šakos sankirtos taško abscisė lygi (pi iš šešių).
Visus šios lygties sprendinius įrašome pagal formulę x = + πk (x lygus pi kartus šeši plius pi ka).
Atsakymas: x = + πk.
Sukurkime funkcijos y = сtg x grafiką.
Apsvarstykite du statybos būdus.
Pirmas būdas yra panašus į funkcijos y = tan x braižymą.
Kadangi ši funkcija yra periodinė, susideda iš begalinio skaičiaus šakų (juostoje tarp x = 0 ir x =π, taip pat juostoje tarp x =π ir x = 2π ir tt) ir nelyginių, sudarysime grafiko dalis taškas po taško intervale nuo nulio iki pi po du (), tada naudosime simetriją ir periodiškumą.
Norėdami sukurti grafiką, naudokime kotangentinių verčių lentelę.
Pažymėkite gautus taškus koordinačių plokštumoje ir sujunkite juos lygia linija.
Kadangi funkcijos grafikas yra santykinai simetriškas, tą pačią šaką sukonstruosime simetriškai.
Taikykime periodiškumą ir gaukime funkcijos y = сtg x grafiką.
Juostoje iš x = 0 ir x =π sukonstravome funkcijos y = сtg x grafiko atšaką. Likusias šakas konstruojame perkeldami sukonstruotą atšaką išilgai x ašies π, - π, 2π, - 2π ir pan.
Antras būdas nubraižydami funkciją y =сtg x.
Lengviausias būdas gauti funkcijos y =сtg x grafiką yra paversti liestinę, naudojant redukcijos formulę (kotangentas x yra lygus x ir pi sumos liestinę atėmus dviem).

Šiuo atveju pirmiausia funkcijos y =tg x grafiko šaką perkeliame išilgai abscisių ašies į dešinę, gauname
y = tg (x+), tada atliekame gauto grafiko simetriją abscisių ašies atžvilgiu. Rezultatas bus funkcijos y =сtg x grafiko atšaka (4 pav.). Žinodami vieną šaką, galime sukurti visą grafiką naudodami funkcijos periodiškumą. Konstruojame likusias šakas, perkeldami sukonstruotą šaką išilgai x ašies π, 2π ir pan.
Funkcijos y =сtg x grafikas taip pat vadinamas tangentoidu, kaip ir funkcijos y =tg x grafikas. Šaka, esanti intervale nuo nulio iki pi, vadinama pagrindine funkcijos y = сtg x grafiko šaka.
Centruota taške A.
α yra kampas, išreikštas radianais.
Tangentas ( įdegis α) yra trigonometrinė funkcija, priklausanti nuo kampo α tarp hipotenuzės ir stačiojo trikampio kojos, lygi priešingos kojos ilgio santykiui |BC| iki gretimos kojos ilgio |AB| .
Kotangentas ( ctg α) yra trigonometrinė funkcija, priklausanti nuo kampo α tarp hipotenuzės ir stačiojo trikampio kojos, lygi gretimos kojos ilgio santykiui |AB| į priešingos kojos ilgį |BC| .
Tangentas
Kur n- visas.
Vakarų literatūroje tangentas žymimas taip:
.
;
;
.
Tangentinės funkcijos grafikas, y = tan x
Kotangentas
Kur n- visas.
Vakarų literatūroje kotangentas žymimas taip:
.
Taip pat priimami šie užrašai:
;
;
.
Kotangentinės funkcijos grafikas, y = ctg x

Tangento ir kotangento savybės
Periodiškumas
Funkcijos y = tg x ir y = ctg x yra periodiniai su periodu π.
Paritetas
Tangentinės ir kotangentinės funkcijos yra nelyginės.
Apibrėžimo ir vertybių sritys didėja, mažėja
Tangentinės ir kotangentinės funkcijos yra tolydžios savo apibrėžimo srityje (žr. tęstinumo įrodymą). Pagrindinės liestinės ir kotangento savybės pateiktos lentelėje ( n- visas).
| y = tg x | y = ctg x | |
| Taikymo sritis ir tęstinumas | ||
| Vertybių diapazonas | -∞ < y < +∞ | -∞ < y < +∞ |
| Didėja | - | |
| Mažėjantis | - | |
| Kraštutinumai | - | - |
| Nuliai, y = 0 | ||
| Sukirtimo taškai su ordinačių ašimi, x = 0 | y = 0 | - |
Formulės
Išraiškos naudojant sinusą ir kosinusą
;
;
;
;
;
Sumos ir skirtumo liestinės ir kotangento formulės
Pavyzdžiui, likusias formules lengva gauti
Tangentų sandauga
Tangentų sumos ir skirtumo formulė
Šioje lentelėje pateikiamos tam tikrų argumento verčių liestinių ir kotangentų reikšmės. 
Išraiškos naudojant kompleksinius skaičius
Išraiškos per hiperbolines funkcijas
;
;
Dariniai
; .
.
N-osios eilės išvestinė funkcijos kintamojo x atžvilgiu:
.
Tangento > > > išvedimo formulės ; kotangentui >>>
Integralai
Serijos išplėtimai
Norėdami gauti x laipsnio liestinės išplėtimą, turite paimti keletą funkcijų plėtimosi laipsnių eilutėje nuodėmė x Ir cos x ir padalinti šiuos daugianario vieni iš kitų, . Taip gaunamos tokios formulės.
Prie .
adresu .
Kur Bn- Bernulio skaičiai. Jie nustatomi iš pasikartojimo santykio:
;
;
Kur.
Arba pagal Laplaso formulę: 
Atvirkštinės funkcijos
Atvirkštinės liestinės ir kotangentinės funkcijos yra atitinkamai arctangentinės ir arkotangentinės.
Arktangentas, arktg
, Kur n- visas.
Arkotangentas, arcctg
, Kur n- visas.
Nuorodos:
I.N. Bronšteinas, K.A. Semendyaev, Matematikos vadovas inžinieriams ir kolegijų studentams, „Lan“, 2009 m.
G. Korn, Matematikos vadovas mokslininkams ir inžinieriams, 2012 m.
, [−5π/2; −3π/2],. . . - vienu žodžiu, visuose segmentuose [−π/2 + 2πk; π/2 + 2πk], kur k Z, ir mažėja visuose segmentuose
[π/2 + 2πn; 3π/2 + 2πn], kur n Z.
11.6 uždavinys. Kuriuose segmentuose funkcija y = cos x didėja, o kuriose mažėja?
11.8 uždavinys. Išdėstykite didėjimo tvarka: sin 1, cos 2, sin 3, cos 4, sin 5, cos 6.
§ 12. Tangento ir kotangento grafikai
Nubraižykime funkciją y = tan x. Pirmiausia sukonstruokime jį skaičiams x, priklausantiems intervalui (−π/2; π/2).
Jei x = 0, tai tan x = 0; kai x padidėja nuo 0 iki π/2, tan x taip pat didėja – tai matyti pažvelgus į liestinės ašį (12.1 pav. a). Kai x artėja prie π/2, lieka mažesnis

Ryžiai. 12.2. y = įdegis x.
π/2, tan x reikšmė didėja (taškas M 12.1 pav. a eina vis aukščiau) ir, aišku, gali tapti savavališkai dideliu teigiamu skaičiumi. Panašiai, x mažėjant nuo 0 iki –π/2, tan x tampa neigiamu skaičiumi, kurio absoliuti reikšmė didėja, kai x artėja prie –π/2. Jei x = π/2 arba −π/2, funkcija tan x yra neapibrėžta. Todėl grafikas y = tan x x (-π/2; π/2) atrodo maždaug taip, kaip parodyta Fig. 12.1 b.
Netoli koordinačių pradžios mūsų kreivė yra arti tiesės y = x x: juk mažiems smailiems kampams apytikslė lygybė tg x ≈ x yra teisinga. Galime sakyti, kad tiesė y = x paliečia funkcijos y = tan x grafiką pradžioje. Be to, 12.1 pav. b kreivė yra simetriška pradžios atžvilgiu. Tai paaiškinama tuo, kad funkcija y = tan x yra nelyginė, tai yra, galioja tapatybė tg(−x) = − tan x.
Norėdami nubraižyti funkciją y = tan x visiems x, prisiminkite, kad tan x yra periodinė funkcija su periodu π. Todėl norint gauti pilną funkcijos y = tan x grafiką, reikia kartoti kreivę pav., be galo daug kartų. 12.1 b, perkeliant jį išilgai abscisių iki atstumų πn, kur n yra sveikas skaičius. Galutinis funkcijos y = tan x grafiko vaizdas yra pav. 12.2.
Pagal grafiką dar kartą matome, kad funkcija y = tan x

Ryžiai. 12.3. y = cotg x.
nėra apibrėžtas x = π/2 + πn, n Z, tai yra tiems x, kuriems cos x = 0. Vertikalios tiesės su lygtimis x = π/2, 3π/2,. . . , prie kurios grafo požiūrio šakos vadinamos grafo asimptotėmis.
Toje pačioje pav. 12.2 pavaizdavome lygties tg x = a sprendinius.
Nubraižykime funkciją y = cot x. Lengviausias būdas yra naudoti redukcijos formulę ctg x = tan(π/2 − x), kad gautumėte šį grafiką iš funkcijos y = tan x grafiko, naudojant transformacijas, panašias į tas, kurias aprašėme ankstesnėje pastraipoje. Rezultatas parodytas fig. 12.3
12.1 problema. Funkcijos y = ctg x grafikas gaunamas iš funkcijos y = tan x grafiko, naudojant simetriją apie tam tikrą tiesę. Kuris? Ar yra kitų linijų su šia nuosavybe?
12.2 uždavinys. Kaip atrodo funkcijos y = cot x grafiko liestinės tiesės lygtis taške su koordinatėmis (π/2; 0)?
12.3 uždavinys. Palyginkite skaičius: a) tg(13π/11) ir tg 3,3π; b) tan 9,6π ir ctg(−11,3π).

12.4 uždavinys. Išdėstykite skaičius didėjančia tvarka: tg 1, tg 2, tg 3, tg 4, tg 5.
12.5 uždavinys. Nubraižykite funkcijas:
a) y = tan(2x − π/3); |
b) y = 2 cot(π/4 − x). |
12.6 uždavinys. Nubraižykite funkcijas: |
|
a) y = arctan x; |
b) y = arcctg x. |
12.7 uždavinys. Nubraižykite funkciją y = arctan x + arctan(1/x).
§ 13. Kas yra sin x + cos x lygus?
Šiame skyriuje bandysime išspręsti šią problemą: kokia yra didžiausia reikšmė, kurią gali turėti išraiška sin x + cos x?
Jei suskaičiavote teisingai, turėjote nustatyti, kad iš visų šioje lentelėje pateiktų x didžiausia reikšmė yra sin x + cos x
gaunamas, kai x yra artimas 45◦ arba radianiniu mastu π/4.
Jei x = π/4, tiksli sin x+cos x reikšmė yra 2. Pasirodo, mūsų rezultatas, gautas eksperimentiniu būdu, ir
iš tikrųjų yra tiesa: visiems x nelygybė sin x + cos x 6 yra teisinga
2, taigi 2 yra didžiausia šios išraiškos priimtina reikšmė.
Kol kas neturime pakankamai priemonių šią nelygybę natūraliausiu būdu įrodyti. Kol kas parodysime, kaip ją sumažinti iki planimetrijos problemos.
Jei 0< x < π/2, то sin x и cos x - катеты прямоугольного треугольника с гипотенузой 1 и острым углом x (рис. 13.1 ).
Todėl mūsų užduotis performuluojama taip: įrodyti, kad stačiojo trikampio su 1 hipotenuze kojų ilgių suma bus didžiausia, jei šis trikampis yra lygiašonis.
13.1 uždavinys. Įrodykite šį teiginį.
Kadangi lygiašonis stačiakampis trikampis su hi-
Potenuzė 1, kojų ilgių suma lygi 2√, šio uždavinio rezultatas reiškia nelygybę sin x + cos x 6 2 visiems x esantiems intervale (0; π/2). Iš čia nesunku padaryti išvadą, kad ši nelygybė galioja visiems x apskritai.
13.1 uždavinio rezultatas galioja ne tik stačiakampiams trikampiams.
13.2 uždavinys. Įrodykite, kad iš visų trikampių su nurodytomis kraštinės AC ir kampo B reikšmėmis didžiausia suma AB + BC bus lygiašoniam trikampiui su pagrindu AC.
Grįžkime prie trigonometrijos.
13.3 uždavinys. Naudodamiesi sinusų lentele iš § 3, sukonstruokite funkcijos y = sin x + cos x taškinį grafiką.
Pastaba. Atminkite, kad x turi būti išreikštas radianais; Jei x reikšmės yra už intervalo ribų, naudokite mažinimo formules.
Jei viską padarėte teisingai, turėtumėte turėti kreivę, kuri atrodo kaip sinusinė banga. Vėliau pamatysime, kad ši kreivė yra ne tik panaši, bet ir sinusoidė. Taip pat išmoksime rasti didžiausias išraiškų reikšmes, tokias kaip 3 sin x + 4 cos x (beje, funkcijos y = 3 sin x + 4 cos x grafikas taip pat yra sinusoidas!).