გაკვეთილი "ფუნქციები y = tgx, y = ctgx, მათი თვისებები და გრაფიკები." გაკვეთილი "ფუნქციები y = tgx, y = ctgx, მათი თვისებები და გრაფიკები" ფუნქციების კვლევა ტანგენტით.
ეს ვიდეო გაკვეთილი განიხილავს ფუნქციების თვისებებს y =ტგx, y = ctgx, გვიჩვენებს, თუ როგორ უნდა ავაშენოთ მათი გრაფიკები.
ვიდეო გაკვეთილი იწყება ფუნქციის ნახვით y =ტგx.
ხაზგასმულია ფუნქციის თვისებები.
1) ფუნქციის დომენი y =ტგxყველა რეალური რიცხვი იწოდება, გარდა x =π/2 + 2 πk. იმათ. გრაფიკზე არ არის წერტილები, რომლებიც მიეკუთვნება ხაზს x =π/2 და x = -π/2, ასევე x = 3π/2 და ასე შემდეგ (იგივე პერიოდულობით). ასე რომ, ფუნქციის გრაფიკი y =ტგxშედგება უსასრულო რაოდენობის ტოტებისაგან, რომლებიც განლაგდება სწორ ხაზებს შორის არსებულ სივრცეებში x = - 3π/2 და x = -π/2, x = -π/2 და x = π/2 და ასე შემდეგ.
2) ფუნქცია y =ტგxპერიოდულია, სადაც ძირითადი პერიოდია π. ეს ადასტურებს თანასწორობას tg(x- π ) = tg x =tg(x+π ) . ეს თანასწორობები ადრე იყო შესწავლილი, ავტორი იწვევს სტუდენტებს გაიხსენონ ისინი და მიუთითოს, რომ ნებისმიერი მართებული მნიშვნელობისთვის ტთანასწორობა მოქმედებს:
tg(t+ π ) = ტგ ტდა გ tg(t+π ) = ctg ტ. ამ ტოლობების შედეგია ის, რომ თუ ფუნქციის გრაფიკის ერთი ტოტი y = tan xხაზებს შორის X = - π/2 და X= π/2, მაშინ დარჩენილი ტოტების მიღება შესაძლებელია ამ ტოტის x ღერძის გასწვრივ გადაადგილებით. π, 2π და ასე შემდეგ.
3) ფუნქცია y =ტგxუცნაურია, რადგან . tg(- x) =- tg x.
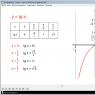
შემდეგი, მოდით გადავიდეთ ფუნქციის გრაფიკის აგებაზე y =ტგx. როგორც ზემოთ აღწერილი ფუნქციის თვისებებიდან ჩანს ფუნქცია y =ტგxპერიოდული და კენტი. მაშასადამე, საკმარისია ავაშენოთ გრაფის ნაწილი - ერთი განშტოება ერთ ინტერვალში, შემდეგ კი გადასატანად გამოიყენოთ სიმეტრია. ავტორი გთავაზობთ ცხრილს, რომელშიც გამოითვლება მნიშვნელობები ტგxგარკვეულ ღირებულებებზე xუფრო ზუსტი შეთქმულებისთვის. ეს წერტილები აღინიშნება კოორდინატთა ღერძზე და დაკავშირებულია გლუვი ხაზით. იმიტომ რომ თუ გრაფიკი სიმეტრიულია კოორდინატების წარმოშობის მიმართ, მაშინ აგებულია იგივე ტოტი, სიმეტრიული კოორდინატების წარმოშობის მიმართ. შედეგად ვიღებთ გრაფიკის ერთ ტოტს y =ტგx. შემდეგ, x ღერძის გასწვრივ გადაადგილების გამოყენებით π, 2 π და ასე შემდეგ, მიიღება გრაფიკი. y =ტგx.
ფუნქციის გრაფიკი y =ტგxეწოდება ტანგენტოიდი, ხოლო ნახატზე ნაჩვენები გრაფიკის სამი ტოტი არის ტანგენტოიდის ძირითადი განშტოებები.
4) ფუნქცია y =ტგxყოველი ინტერვალით (- + ; +) იზრდება.
5) ფუნქციის გრაფიკი y =ტგxარ აქვს შეზღუდვები ზემოთ და ქვემოთ.
6) ფუნქცია y =ტგxარ აქვს უდიდესი და უმცირესი ღირებულება.
7) ფუნქცია y =ტგxუწყვეტი ნებისმიერ ინტერვალზე (- - π/2+π;π/2+π). სწორ ხაზს π/2+π ეწოდება ფუნქციის გრაფიკის ასიმპტოტს y =ტგx, იმიტომ ამ წერტილებში ფუნქციის გრაფიკი წყდება.
8) ფუნქციის მნიშვნელობების ნაკრები y =ტგxყველა რეალური რიცხვი იწოდება.
შემდგომ ვიდეო გაკვეთილში მოცემულია მაგალითი: ამოხსენით განტოლება ტგx. ამოსახსნელად ავაშენებთ ფუნქციის 2 გრაფიკს ზედა იპოვეთ ამ გრაფიკების გადაკვეთის წერტილები: ეს არის წერტილების უსასრულო ნაკრები, რომელთა აბსციები განსხვავდება πk-ით. ამ განტოლების ფესვი იქნება X= π/6 +πk.
განვიხილოთ ფუნქციის გრაფიკი y =ctgx. ფუნქციის გრაფიკის დახატვა შესაძლებელია ორი გზით.
პირველი მეთოდი გულისხმობს გრაფიკის აგებას, როგორც გრაფის აგებას ფუნქციები y =ტგx. ავაშენოთ ფუნქციის გრაფიკის ერთი ტოტი y = გტგxხაზებს შორის X= 0u X= π. შემდეგ სიმეტრიისა და პერიოდულობის გამოყენებით ავაშენებთ გრაფიკის სხვა ტოტებს.
მეორე მეთოდი უფრო მარტივია. ფუნქციის გრაფიკი y = сtgxშეიძლება მივიღოთ ტანგენტების გარდაქმნით შემცირების ფორმულის გამოყენებით თანtgx = - tg(x +π/2). ამისათვის გადავიტანოთ ფუნქციის გრაფიკის ერთი ტოტი y = tgx x-ღერძის გასწვრივ π/2 მარჯვნივ. დარჩენილი ტოტები მიიღება ამ ტოტის x ღერძის გასწვრივ π, 2π და ა.შ. y = ctg ფუნქციის გრაფიკი xმას ასევე უწოდებენ ტანგენტოიდს, ხოლო გრაფიკის ტოტი (0;π) ინტერვალში არის ტანგენტოიდის მთავარი განშტოება.
ტექსტის გაშიფვრა:
განვიხილავთ y = tan x ფუნქციის თვისებებს (y უდრის ტანგენტს x), y = ctg x (y უდრის კოტანგენტს x) და ავაშენებთ მათ გრაფიკებს. განვიხილოთ ფუნქცია y = tgx

y = tan x ფუნქციის გამოსახვამდე ჩამოვწეროთ ამ ფუნქციის თვისებები.
თვისება 1. y = tan x ფუნქციის განსაზღვრის დომენი არის ყველა რეალური რიცხვი, გარდა x = + πk ფორმის რიცხვებისა (x უდრის pi ორზე და pi ka-ს ჯამს).
ეს ნიშნავს, რომ ამ ფუნქციის გრაფიკზე არ არის წერტილები, რომლებიც მიეკუთვნება x = წრფეს (ვიღებთ, თუ k = 0 ka ნულის ტოლია) და წრფე x = (x უდრის მინუს pi ორზე) (ჩვენ მიიღეთ, თუ k = - 1 ka უდრის მინუს ერთს), და სწორი ხაზი x = (x უდრის სამ პი ორს) (ვიღებთ, თუ k = 1 უდრის ერთს) და ა.შ. ეს ნიშნავს, რომ გრაფიკი ფუნქციის y = tan x შედგება უსასრულო რაოდენობის ტოტებისაგან, რომლებიც განლაგდება სწორ ხაზებს შორის ინტერვალებში. კერძოდ, ზოლში x = და x =- შორის; ზოლში x = - და x = ; ზოლში x = და x = და ასე უსასრულოდ.
თვისება 2. ფუნქცია y = tan x პერიოდულია ძირითადი პერიოდით π. (რადგან ორმაგი თანასწორობა მართალია
tan(x- π) = tanx = tan (x+π) x-ის მინუს pi-ის ტანგენსი უდრის x-ის ტანგენტს და ტოლია x-ის ტანგენტს პლუს pi). ეს თანასწორობა გავითვალისწინეთ ტანგენტისა და კოტანგენტის შესწავლისას. შევახსენოთ მას:
t-ის ნებისმიერი დასაშვები მნიშვნელობისთვის ტოლობები მოქმედებს:
tg (t + π) = tgt
ctg (t + π) = ctgt
ამ თანასწორობიდან გამომდინარეობს, რომ y = tan x ფუნქციის გრაფიკის ტოტის აგების შემდეგ x = - და x = ინტერვალში, ჩვენ ვიღებთ დარჩენილ ტოტებს X ღერძის გასწვრივ აგებული ტოტის გადაადგილებით π, 2π-ით. , და ასე შემდეგ.
თვისება 3. ფუნქცია y = tan x არის კენტი ფუნქცია, ვინაიდან ტოლობა tg (- x) = - tan x მართალია.
დავხატოთ ფუნქცია y = tan x
ვინაიდან ეს ფუნქცია პერიოდულია, შედგება უსასრულო რაოდენობის ტოტებისაგან (ზოლში x = და x = შორის, ასევე ზოლში x = და x = და ა.შ.) და კენტი, ჩვენ ავაშენებთ ნაწილს ნულიდან პი-მდე ინტერვალის გრაფიკი წერტილი-პუნქტით ორი (), შემდეგ გამოიყენეთ საწყისისა და პერიოდულობის სიმეტრია.
მოდით ავაშენოთ ტანგენტების მნიშვნელობების ცხრილი ნახატებისთვის.
ჩვენ ვპოულობთ პირველ წერტილს: ვიცით, რომ x = 0 tan x = 0 (x უდრის ნულს, tan x ასევე ნულის ტოლია); შემდეგი წერტილი: x = tan x = (x უდრის pi-ს ექვსზე, ტანგენსი x უდრის ფესვს სამის სამზე); მოდით აღვნიშნოთ შემდეგი პუნქტები: x = tan x = 1 (x უდრის pi ოთხი tan x უდრის ერთს), და x = tg x = (x უდრის pi სამ tan x უდრის კვადრატულ ფესვს. სამი). მონიშნეთ მიღებული წერტილები კოორდინატულ სიბრტყეზე და შეაერთეთ ისინი გლუვი ხაზით (ნახ. 2).
ვინაიდან ფუნქციის გრაფიკი სიმეტრიულია კოორდინატების წარმოშობის მიმართ, ჩვენ ავაშენებთ იმავე ტოტს სიმეტრიულად კოორდინატების წარმოშობის მიმართ. (ნახ. 3).
და ბოლოს, პერიოდულობის გამოყენებით, ვიღებთ y = tan x ფუნქციის გრაფიკს.
ჩვენ ავაშენეთ y = tan x ფუნქციის გრაფიკის ტოტი ზოლში x = - და x =-დან. დარჩენილ ტოტებს ვაშენებთ აგებული ტოტის X ღერძის გასწვრივ π, 2π და ა.შ.

შექმნილ ნაკვეთს ტანგენტოიდი ეწოდება.
მე-3 სურათზე ნაჩვენები ტანგენტოიდის ნაწილს ტანგენტოიდის მთავარი განშტოება ეწოდება.
გრაფიკის საფუძველზე ჩვენ ჩამოვწერთ ამ ფუნქციის კიდევ რამდენიმე თვისებას.
თვისება 4. ფუნქცია y = tan x იზრდება თითოეულ ინტერვალზე (მინუს pi-დან ორი პლუს pi ka-მდე ორი პლუს pi ka-მდე).
თვისება 5. ფუნქცია y = tan x არ არის შემოსაზღვრული არც ზემოთ და არც ქვემოთ.
თვისება 6. ფუნქციას y = tan x არ აქვს არც უდიდესი და არც უმცირესი მნიშვნელობები.
თვისება 7. ფუნქცია y = tan x უწყვეტია ფორმის ნებისმიერ ინტერვალზე (მინუს pi-დან ორი პლუს pi ka-მდე ორი პლუს pi ka-მდე).
x = + πk ფორმის სწორი ხაზი (x უდრის pi-ს ჯამს ორზე და pi ka-ზე) არის ფუნქციის გრაფიკის ვერტიკალური ასიმპტოტი, ვინაიდან x = + πk ფორმის წერტილებში ფუნქცია განიცდის a. უწყვეტობა.
თვისება 8. y = tan x ფუნქციის მნიშვნელობების სიმრავლე ყველა რეალური რიცხვია, ანუ (e-დან eff უდრის ინტერვალს მინუს უსასრულობიდან პლუს უსასრულობამდე).
მაგალითი 1. ამოხსენით განტოლება tg x = (ტანგენსი x უდრის ფესვს სამი სამზე).
გამოსავალი. ავაშენოთ y = tan x ფუნქციების გრაფიკები ერთ კოორდინატულ სისტემაში
(y უდრის x-ის ტანგენტს) და y = (y უდრის სამის ფესვს გაყოფილი სამზე).
მივიღეთ უსასრულოდ ბევრი გადაკვეთის წერტილი, რომელთა აბსციზა ერთმანეთისგან განსხვავდება πk-ით (pi ka), ვინაიდან tg x = x =-ზე, მაშინ მთავარ განშტოებაზე გადაკვეთის წერტილის აბსციზა უდრის (pi ექვსით).
ჩვენ ვწერთ ამ განტოლების ყველა ამონახსანს x = + πk ფორმულით (x უდრის pi გამრავლებული ექვს პლუს pi ka).
პასუხი: x = + πk.
ავაშენოთ y = сtg x ფუნქციის გრაფიკი.
განვიხილოთ მშენებლობის ორი მეთოდი.
პირველი გზამსგავსია y = tan x ფუნქციის შედგენის.
ვინაიდან ეს ფუნქცია პერიოდულია, შედგება უსასრულო რაოდენობის ტოტებისაგან (ზოლში x = 0 და x =π შორის, ასევე ზოლში x =π და x = 2π და ა.შ.) და კენტი, ჩვენ ავაშენებთ გრაფიკის ნაწილი წერტილი-პუნქტი ნულიდან პიის ინტერვალზე ორი (), მაშინ გამოვიყენებთ სიმეტრიას და პერიოდულობას.
მოდით გამოვიყენოთ კოტანგენტების მნიშვნელობების ცხრილი გრაფიკის ასაგებად.
მონიშნეთ მიღებული წერტილები კოორდინატულ სიბრტყეზე და დააკავშირეთ ისინი გლუვი ხაზით.
ვინაიდან ფუნქციის გრაფიკი შედარებით სიმეტრიულია, ჩვენ ავაშენებთ იმავე ტოტს სიმეტრიულად.
გამოვიყენოთ პერიოდულობა და მივიღოთ y = сtg x ფუნქციის გრაფიკი.
ჩვენ ავაშენეთ y = сtg x ფუნქციის გრაფიკის ტოტი ზოლში x = 0 და x =π. დარჩენილ ტოტებს ვაშენებთ აგებული ტოტის x ღერძის გასწვრივ π, - π, 2π, - 2π და ა.შ.
მეორე გზა y =сtg x ფუნქციის გამოსახვა.
y =сtg x ფუნქციის გრაფიკის მისაღებად უმარტივესი გზაა ტანგენსის გარდაქმნა შემცირების ფორმულის გამოყენებით (კოტანგენსი x უდრის x და pi ჯამის ტანგენსს გამოკლებული ორზე).

ამ შემთხვევაში, ჯერ გადავიტანთ y =tg x ფუნქციის გრაფიკის ტოტს აბსცისის ღერძის გასწვრივ მარჯვნივ, მივიღებთ
y = tg (x+) და შემდეგ ვასრულებთ მიღებული გრაფიკის სიმეტრიას აბსცისის ღერძთან მიმართებაში. შედეგი იქნება y =сtg x ფუნქციის გრაფიკის განშტოება (ნახ. 4). ერთი ტოტის ცოდნით, ჩვენ შეგვიძლია ავაშენოთ მთელი გრაფიკი ფუნქციის პერიოდულობის გამოყენებით. ჩვენ ვაშენებთ დარჩენილ ტოტებს აგებული ტოტის x ღერძის გასწვრივ π, 2π და ა.შ.
y =сtg x ფუნქციის გრაფიკს ასევე უწოდებენ ტანგენტოიდს, ისევე როგორც y =tg x ფუნქციის გრაფიკს. ტოტს, რომელიც დევს ნულიდან pi-მდე ინტერვალში, ეწოდება y = сtg x ფუნქციის გრაფიკის მთავარი განშტოება.
ცენტრირებულია A წერტილში.
α არის რადიანებში გამოხატული კუთხე.
ტანგენტი ( tan α) არის ტრიგონომეტრიული ფუნქცია, რომელიც დამოკიდებულია კუთხიდან α ჰიპოტენუზასა და მართკუთხა სამკუთხედის წვერს შორის, უდრის მოპირდაპირე ფეხის სიგრძის თანაფარდობას |BC| მიმდებარე ფეხის სიგრძემდე |AB| .
კოტანგენსი ( ctg α) არის ტრიგონომეტრიული ფუნქცია, რომელიც დამოკიდებულია კუთხიდან α ჰიპოტენუზასა და მართკუთხა სამკუთხედის წვერს შორის, ტოლია მიმდებარე ფეხის სიგრძის თანაფარდობის |AB| მოპირდაპირე ფეხის სიგრძემდე |ძვ.წ.| .
ტანგენტი
სად ნ- მთელი.
დასავლურ ლიტერატურაში ტანგენტი შემდეგნაირად აღინიშნება:
.
;
;
.
ტანგენტის ფუნქციის გრაფიკი, y = tan x
Cotangent
სად ნ- მთელი.
დასავლურ ლიტერატურაში კოტანგენტს აღნიშნავენ შემდეგნაირად:
.
ასევე მიღებულია შემდეგი აღნიშვნები:
;
;
.
კოტანგენსი ფუნქციის გრაფიკი, y = ctg x

ტანგენსის და კოტანგენსის თვისებები
პერიოდულობა
ფუნქციები y = tg xდა y = ctg xპერიოდულია π პერიოდით.
პარიტეტი
ტანგენსი და კოტანგენსი ფუნქციები უცნაურია.
განსაზღვრებისა და ღირებულებების სფეროები, მზარდი, კლებადი
ტანგენსი და კოტანგენსი ფუნქციები უწყვეტია მათი განმარტების სფეროში (იხ. უწყვეტობის მტკიცებულება). ტანგენტისა და კოტანგენსის ძირითადი თვისებები მოცემულია ცხრილში ( ნ- მთელი).
| y= tg x | y= ctg x | |
| მასშტაბები და უწყვეტობა | ||
| ღირებულებების დიაპაზონი | -∞ < y < +∞ | -∞ < y < +∞ |
| მზარდი | - | |
| Დაღმავალი | - | |
| უკიდურესობები | - | - |
| ნულები, y = 0 | ||
| კვეთის წერტილები ორდინატთა ღერძით, x = 0 | y= 0 | - |
ფორმულები
გამონათქვამები სინუსის და კოსინუსის გამოყენებით
;
;
;
;
;
ტანგენტებისა და კოტანგენტების ფორმულები ჯამიდან და სხვაობიდან
დანარჩენი ფორმულების მიღება მარტივია, მაგალითად
Tangents- ის პროდუქტი
ტანგენტების ჯამისა და სხვაობის ფორმულა
ამ ცხრილში მოცემულია ტანგენტებისა და კოტანგენტების მნიშვნელობები არგუმენტის გარკვეული მნიშვნელობებისთვის. 
გამოთქმები რთული რიცხვების გამოყენებით
გამოხატვები ჰიპერბოლური ფუნქციების საშუალებით
;
;
წარმოებულები
; .
.
n-ე რიგის წარმოებული ფუნქციის x ცვლადის მიმართ:
.
ტანგენტების ფორმულების გამოყვანა > > > ; კოტანგენტისთვის >>>
ინტეგრალები
სერიის გაფართოებები
x-ის სიმძლავრეებში ტანგენსის გაფართოების მისაღებად, თქვენ უნდა აიღოთ გაფართოების რამდენიმე ტერმინი სიმძლავრის სერიაში ფუნქციებისთვის. ცოდვა xდა cos xდა გავყოთ ეს მრავალწევრები ერთმანეთზე, . ეს აწარმოებს შემდეგ ფორმულებს.
ზე.
ზე.
სად ბნ- ბერნულის ნომრები. ისინი განისაზღვრება ან განმეორებითი ურთიერთობით:
;
;
სად .
ან ლაპლასის ფორმულის მიხედვით: 
ინვერსიული ფუნქციები
ტანგენტისა და კოტანგენსის შებრუნებული ფუნქციებია, შესაბამისად, არქტანგენსი და არკოტანგენსი.
არქტანგენტი, არქტგ
, სად ნ- მთელი.
Arccotangent, arcctg
, სად ნ- მთელი.
ცნობები:
ი.ნ. ბრონშტეინი, კ.ა. სემენდიაევი, მათემატიკის სახელმძღვანელო ინჟინრებისა და კოლეჯის სტუდენტებისთვის, „ლან“, 2009 წ.
G. Korn, მათემატიკის სახელმძღვანელო მეცნიერთა და ინჟინრებისთვის, 2012 წ.
, [−5π/2; −3π/2],. . . - ერთი სიტყვით, ყველა სეგმენტზე [−π/2 + 2πk; π/2 + 2πk], სადაც k Z და მცირდება ყველა სეგმენტზე
[π/2 + 2πn; 3π/2 + 2πn], სადაც n Z.
პრობლემა 11.6. რომელ სეგმენტებზე იზრდება ფუნქცია y = cos x და რომელზე მცირდება?
პრობლემა 11.8. დაალაგეთ ზრდადი თანმიმდევრობით: sin 1, cos 2, sin 3, cos 4, sin 5, cos 6.
§ 12. ტანგენსის და კოტანგენსის გრაფიკები
დავხატოთ ფუნქცია y = tan x. პირველი, მოდით ავაშენოთ ის x რიცხვებისთვის, რომლებიც მიეკუთვნებიან ინტერვალს (−π/2; π/2).
თუ x = 0, მაშინ tan x = 0; როდესაც x იზრდება 0-დან π/2-მდე, tan x ასევე იზრდება - ეს ჩანს, თუ ტანგენტის ღერძს დააკვირდებით (ნახ. 12.1 ა). როგორც x უახლოვდება π/2, რჩება უფრო პატარა

ბრინჯი. 12.2. y = tan x.
π/2, tan x-ის მნიშვნელობა იზრდება (პუნქტი M ნახ. 12.1-ზე a მაღლა და მაღლა ეშვება) და, ცხადია, შეიძლება გახდეს თვითნებურად დიდი დადებითი რიცხვი. ანალოგიურად, როგორც x 0-დან −π/2-მდე მცირდება, tan x ხდება უარყოფითი რიცხვი, რომლის აბსოლუტური მნიშვნელობა იზრდება როგორც x უახლოვდება −π/2. x = π/2 ან −π/2-ისთვის, ფუნქცია tan x განუსაზღვრელია. მაშასადამე, გრაფიკი y = tan x x-ისთვის (−π/2; π/2) დაახლოებით ისე გამოიყურება, როგორც ნახ. 12.1 ბ.
კოორდინატების საწყისთან ახლოს, ჩვენი მრუდი ახლოს არის y = x x სწორ ხაზთან: ბოლოს და ბოლოს, მცირე მახვილი კუთხისთვის, სავარაუდო ტოლობა tg x ≈ x მართალია. შეგვიძლია ვთქვათ, რომ y = x წრფე ეხება საწყისზე y = tan x ფუნქციის გრაფიკს. გარდა ამისა, ნახ. 12.1 b-ის მრუდი სიმეტრიულია საწყისის მიმართ. ეს აიხსნება იმით, რომ ფუნქცია y = tan x არის უცნაური, ანუ იდენტურობა tg(−x) = − tan x მოქმედებს.
y = tan x ფუნქციის გამოსათვლელად ყველა x-ისთვის, გავიხსენოთ, რომ tan x არის პერიოდული ფუნქცია π პერიოდით. ამიტომ y = tan x ფუნქციის სრული გრაფიკის მისაღებად საჭიროა ნახ. მრუდის უსასრულოდ ბევრჯერ გამეორება. 12.1 b, გადაადგილება აბსცისის გასწვრივ πn დისტანციებზე, სადაც n არის მთელი რიცხვი. y = tan x ფუნქციის გრაფიკის საბოლოო ხედვა მოცემულია ნახ. 12.2.
გრაფიკის მიხედვით კიდევ ერთხელ ვხედავთ, რომ ფუნქცია y = tan x

ბრინჯი. 12.3. y = cotg x.
არ არის განსაზღვრული x = π/2 + πn, n Z, ანუ იმ x-სთვის, რომლისთვისაც cos x = 0. ვერტიკალური ხაზები განტოლებით x = π/2, 3π/2,. . . , რომლის მიმართაც გრაფის მიდგომის ტოტებს გრაფის ასიმპტოტები ეწოდება.
იმავე ნახ. 12.2 ჩვენ გამოვსახეთ tg x = a განტოლების ამონახსნები.
დავხატოთ ფუნქცია y = cot x. უმარტივესი გზაა გამოვიყენოთ შემცირების ფორმულა ctg x = tan(π/2 − x) ამ გრაფიკის მისაღებად y = tan x ფუნქციის გრაფიკიდან, წინა აბზაცში აღწერილის მსგავსი გარდაქმნების გამოყენებით. შედეგი ნაჩვენებია ნახ. 12.3
პრობლემა 12.1. y = ctg x ფუნქციის გრაფიკი მიღებულია y = tan x ფუნქციის გრაფიკიდან გარკვეული წრფის სიმეტრიის გამოყენებით. Რომელი? არის სხვა ხაზები ამ ქონებასთან?
პრობლემა 12.2. როგორ გამოიყურება y = cot x ფუნქციის გრაფიკზე ტანგენსი სწორი ხაზის განტოლება კოორდინატების მქონე წერტილში (π/2; 0)?
პრობლემა 12.3. შეადარეთ რიცხვები: ა) tg(13π/11) და tg 3.3π; ბ) რუჯი 9,6π და ctg(−11,3π).

პრობლემა 12.4. დაალაგე რიცხვები ზრდის მიხედვით: tg 1, tg 2, tg 3, tg 4, tg 5.
პრობლემა 12.5. ფუნქციების გრაფიკის დახატვა:
ა) y = tan(2x − π/3); |
ბ) y = 2 cot (π/4 − x). |
პრობლემა 12.6. ფუნქციების გრაფიკის დახატვა: |
|
ა) y = არქტანი x; |
ბ) y = arcctg x. |
პრობლემა 12.7. დახაზეთ ფუნქცია y = arctan x + arctan(1/x).
§ 13. რისი ტოლია sin x + cos x?
ამ განყოფილებაში შევეცდებით გადავჭრათ შემდეგი პრობლემა: რა არის ყველაზე დიდი მნიშვნელობა, რომელიც შეიძლება მიიღოს გამოხატულება sin x + cos x?
თუ სწორად დათვალეთ, უნდა გეპოვათ, რომ ამ ცხრილის ყველა x-დან ყველაზე დიდი მნიშვნელობა არის sin x + cos x.
მიიღება x-ისთვის 45◦-თან ახლოს, ან რადიანის ზომით, π/4-მდე.
თუ x = π/4, sin x+cos x-ის ზუსტი მნიშვნელობა არის 2. გამოდის, რომ ექსპერიმენტულად მიღებული ჩვენი შედეგი და
ფაქტიურად ჭეშმარიტია: x ყველასთვის უტოლობა sin x + cos x 6 არის ჭეშმარიტი
2, ანუ 2 არის ყველაზე დიდი მნიშვნელობა, რომელიც მიღებულია ამ გამონათქვამით.
ჩვენ ჯერ არ გვაქვს საკმარისი საშუალება ამ უთანასწორობის ყველაზე ბუნებრივი გზით დასამტკიცებლად. ამ დროისთვის ჩვენ გაჩვენებთ, თუ როგორ შევიყვანოთ იგი პლანიმეტრიის პრობლემამდე.
თუ 0< x < π/2, то sin x и cos x - катеты прямоугольного треугольника с гипотенузой 1 и острым углом x (рис. 13.1 ).
მაშასადამე, ჩვენი დავალება გადაფორმებულია შემდეგნაირად: დავამტკიცოთ, რომ მართკუთხა სამკუთხედის კიდეების სიგრძის ჯამი ჰიპოტენუზა 1-ით მაქსიმალური იქნება, თუ ეს სამკუთხედი ტოლფერდაა.
პრობლემა 13.1. დაამტკიცეთ ეს განცხადება.
ვინაიდან ტოლფერდა მართკუთხა სამკუთხედი hy-
პოტენუზა 1, ფეხების სიგრძის ჯამი უდრის 2√-ს, ამ ამოცანის შედეგი გულისხმობს უტოლობას sin x + cos x 6 2 ყველა x-ისთვის, რომელიც დევს ინტერვალში (0; π/2). აქედან ძნელი არ არის დავასკვნათ, რომ ეს უტოლობა მოქმედებს ზოგადად ყველა x-ზე.
13.1 ამოცანის შედეგი არ შეესაბამება მხოლოდ მართკუთხა სამკუთხედებს.
პრობლემა 13.2. დაამტკიცეთ, რომ ყველა სამკუთხედს შორის AC გვერდის და B კუთხის მოცემული მნიშვნელობებით, უდიდესი ჯამი AB + BC იქნება AC ფუძის მქონე ტოლფერდა სამკუთხედისთვის.
დავუბრუნდეთ ტრიგონომეტრიას.
პრობლემა 13.3. სინუსების ცხრილის გამოყენებით § 3-დან შექმენით y = sin x + cos x ფუნქციის წერტილი-პუნქტიანი გრაფიკი.
Შენიშვნა. გახსოვდეთ, რომ x უნდა იყოს გამოხატული რადიანებით; x მნიშვნელობებისთვის ინტერვალის გარეთ გამოიყენეთ შემცირების ფორმულები.
თუ ყველაფერი სწორად გააკეთე, უნდა გქონდეს მრუდი, რომელიც ჰგავს სინუს ტალღას. მოგვიანებით დავინახავთ, რომ ეს მრუდი არა მხოლოდ მსგავსია, არამედ არის სინუსოიდი. ჩვენ ასევე ვისწავლით ისეთი გამონათქვამების უდიდესი მნიშვნელობების პოვნას, როგორიცაა 3 sin x + 4 cos x (სხვათა შორის, ფუნქციის y = 3 sin x + 4 cos x ასევე სინუსოიდია!).