The amount in the denominator. Getting rid of irrationality in the denominator of a fraction. Basic steps to get rid of irrationality in the denominator of a fraction

When transforming a fractional algebraic expression whose denominator contains an irrational expression, one usually tries to represent the fraction so that its denominator is rational. If A,B,C,D,... are some algebraic expressions, then you can specify rules with the help of which you can get rid of radical signs in the denominator of expressions of the form

In all these cases, liberation from irrationality is achieved by multiplying the numerator and denominator of the fraction by a factor chosen so that its product by the denominator of the fraction is rational.

1) To get rid of irrationality in the denominator of a fraction of the form . In multiply the numerator and denominator by

Example 1. .

2) In the case of fractions of the form . Multiply the numerator and denominator by an irrational factor

respectively, i.e. to the conjugate irrational expression.

The meaning of the last action is that in the denominator the product of the sum and the difference is transformed into a difference of squares, which will already be a rational expression.

Example 2. Free yourself from irrationality in the denominator of the expression:

Solution, a) Multiply the numerator and denominator of the fraction by the expression . We get (provided that)

3) In the case of expressions like

the denominator is treated as a sum (difference) and multiplied by the partial square of the difference (sum) to obtain the sum (difference) of cubes ((20.11), (20.12)). The numerator is also multiplied by the same factor.

Example 3. Free yourself from irrationality in the denominator of expressions:

Solution, a) Considering the denominator of this fraction as the sum of the numbers and 1, multiply the numerator and denominator by the partial square of the difference of these numbers:

or finally:

In some cases, it is necessary to perform a transformation of the opposite nature: to free the fraction from irrationality in the numerator. It is carried out in exactly the same way.

Example 4. Free yourself from irrationality in the numerator of a fraction.

In this topic we will consider all three groups of limits with irrationality listed above. Let's start with limits containing uncertainty of the form $\frac(0)(0)$.

Uncertainty disclosure $\frac(0)(0)$.

The solution to standard examples of this type usually consists of two steps:

We get rid of the irrationality that caused uncertainty by multiplying by the so-called “conjugate” expression;
If necessary, factor the expression in the numerator or denominator (or both);
We reduce the factors leading to uncertainty and calculate the desired value of the limit.

The term "conjugate expression" used above will be explained in detail in the examples. For now there is no reason to dwell on it in detail. In general, you can go the other way, without using the conjugate expression. Sometimes a well-chosen replacement can eliminate irrationality. Such examples are rare in standard tests, so we will consider only one example No. 6 for the use of replacement (see the second part of this topic).

We will need several formulas, which I will write down below:

\begin(equation) a^2-b^2=(a-b)\cdot(a+b) \end(equation) \begin(equation) a^3-b^3=(a-b)\cdot(a^2 +ab+b^2) \end(equation) \begin(equation) a^3+b^3=(a+b)\cdot(a^2-ab+b^2) \end(equation) \begin (equation) a^4-b^4=(a-b)\cdot(a^3+a^2 b+ab^2+b^3)\end(equation)

In addition, we assume that the reader knows the formulas for solving quadratic equations. If $x_1$ and $x_2$ are the roots of the quadratic trinomial $ax^2+bx+c$, then it can be factorized using the following formula:

\begin(equation) ax^2+bx+c=a\cdot(x-x_1)\cdot(x-x_2) \end(equation)

Formulas (1)-(5) are quite sufficient for solving standard problems, which we will now move on to.

Example No. 1

Find $\lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)$.

Since $\lim_(x\to 3)(\sqrt(7-x)-2)=\sqrt(7-3)-2=\sqrt(4)-2=0$ and $\lim_(x\ to 3) (x-3)=3-3=0$, then in the given limit we have an uncertainty of the form $\frac(0)(0)$. The difference $\sqrt(7-x)-2$ prevents us from revealing this uncertainty. In order to get rid of such irrationalities, multiplication by the so-called “conjugate expression” is used. We will now look at how such multiplication works. Multiply $\sqrt(7-x)-2$ by $\sqrt(7-x)+2$:

$$(\sqrt(7-x)-2)(\sqrt(7-x)+2)$$

To open the brackets, apply , substituting $a=\sqrt(7-x)$, $b=2$ into the right side of the mentioned formula:

$$(\sqrt(7-x)-2)(\sqrt(7-x)+2)=(\sqrt(7-x))^2-2^2=7-x-4=3-x .$$

As you can see, if you multiply the numerator by $\sqrt(7-x)+2$, then the root (i.e., irrationality) in the numerator will disappear. This expression $\sqrt(7-x)+2$ will be conjugate to the expression $\sqrt(7-x)-2$. However, we cannot simply multiply the numerator by $\sqrt(7-x)+2$, because this will change the fraction $\frac(\sqrt(7-x)-2)(x-3)$ under the limit . You need to multiply both the numerator and denominator at the same time:

$$ \lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)= \left|\frac(0)(0)\right|=\lim_(x\to 3)\frac((\sqrt(7-x)-2)\cdot(\sqrt(7-x)+2))((x-3)\cdot(\sqrt(7-x)+2)) $$

Now remember that $(\sqrt(7-x)-2)(\sqrt(7-x)+2)=3-x$ and open the brackets. And after opening the parentheses and a small transformation $3-x=-(x-3)$, we reduce the fraction by $x-3$:

$$ \lim_(x\to 3)\frac((\sqrt(7-x)-2)\cdot(\sqrt(7-x)+2))((x-3)\cdot(\sqrt( 7-x)+2))= \lim_(x\to 3)\frac(3-x)((x-3)\cdot(\sqrt(7-x)+2))=\\ =\lim_ (x\to 3)\frac(-(x-3))((x-3)\cdot(\sqrt(7-x)+2))= \lim_(x\to 3)\frac(-1 )(\sqrt(7-x)+2) $$

The uncertainty $\frac(0)(0)$ has disappeared. Now you can easily get the answer of this example:

$$ \lim_(x\to 3)\frac(-1)(\sqrt(7-x)+2)=\frac(-1)(\sqrt(7-3)+2)=-\frac( 1)(\sqrt(4)+2)=-\frac(1)(4).$$

I note that the conjugate expression can change its structure - depending on what kind of irrationality it should remove. In examples No. 4 and No. 5 (see the second part of this topic) a different type of conjugate expression will be used.

Answer: $\lim_(x\to 3)\frac(\sqrt(7-x)-2)(x-3)=-\frac(1)(4)$.

Example No. 2

Find $\lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))$.

Since $\lim_(x\to 2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=\sqrt(2^2+5)-\sqrt(7\cdot 2 ^2-19)=3-3=0$ and $\lim_(x\to 2)(3x^2-5x-2)=3\cdot2^2-5\cdot 2-2=0$, then we we are dealing with uncertainty of the form $\frac(0)(0)$. Let's get rid of the irrationality in the denominator of this fraction. To do this, we add both the numerator and denominator of the fraction $\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))$ to the expression $\sqrt(x^ 2+5)+\sqrt(7x^2-19)$ conjugate to the denominator:

$$ \lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=\left|\frac(0 )(0)\right|= \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19))) ((\sqrt(x^2+5)-\sqrt(7x^2-19))(\sqrt(x^2+5)+\sqrt(7x^2-19))) $$

Again, as in example No. 1, you need to use parentheses to expand. Substituting $a=\sqrt(x^2+5)$, $b=\sqrt(7x^2-19)$ into the right side of the mentioned formula, we obtain the following expression for the denominator:

$$ \left(\sqrt(x^2+5)-\sqrt(7x^2-19)\right)\left(\sqrt(x^2+5)+\sqrt(7x^2-19)\ right)=\\ =\left(\sqrt(x^2+5)\right)^2-\left(\sqrt(7x^2-19)\right)^2=x^2+5-(7x ^2-19)=-6x^2+24=-6\cdot(x^2-4) $$

Let's return to our limit:

$$ \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)))((\sqrt(x ^2+5)-\sqrt(7x^2-19))(\sqrt(x^2+5)+\sqrt(7x^2-19)))= \lim_(x\to 2)\frac( (3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)))(-6\cdot(x^2-4))=\\ =-\ frac(1)(6)\cdot \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2-19)) )(x^2-4) $$

In example No. 1, almost immediately after multiplication by the conjugate expression, the fraction was reduced. Here, before the reduction, you will have to factorize the expressions $3x^2-5x-2$ and $x^2-4$, and only then proceed to the reduction. To factor the expression $3x^2-5x-2$ you need to use . First, let's solve the quadratic equation $3x^2-5x-2=0$:

$$ 3x^2-5x-2=0\\ \begin(aligned) & D=(-5)^2-4\cdot3\cdot(-2)=25+24=49;\\ & x_1=\ frac(-(-5)-\sqrt(49))(2\cdot3)=\frac(5-7)(6)=-\frac(2)(6)=-\frac(1)(3) ;\\ & x_2=\frac(-(-5)+\sqrt(49))(2\cdot3)=\frac(5+7)(6)=\frac(12)(6)=2. \end(aligned) $$

Substituting $x_1=-\frac(1)(3)$, $x_2=2$ into , we will have:

$$ 3x^2-5x-2=3\cdot\left(x-\left(-\frac(1)(3)\right)\right)(x-2)=3\cdot\left(x+\ frac(1)(3)\right)(x-2)=\left(3\cdot x+3\cdot\frac(1)(3)\right)(x-2) =(3x+1)( x-2). $$

Now it’s time to factorize the expression $x^2-4$. Let's use , substituting $a=x$, $b=2$ into it:

$$ x^2-4=x^2-2^2=(x-2)(x+2) $$

Let's use the results obtained. Since $x^2-4=(x-2)(x+2)$ and $3x^2-5x-2=(3x+1)(x-2)$, then:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x^2-5x-2)(\sqrt(x^2+5)+\sqrt(7x^2 -19)))(x^2-4) =-\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(x-2)(\sqrt(x ^2+5)+\sqrt(7x^2-19)))((x-2)(x+2)) $$

Reducing by the bracket $x-2$ we get:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(x-2)(\sqrt(x^2+5)+\sqrt(7x^ 2-19)))((x-2)(x+2)) =-\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(\sqrt( x^2+5)+\sqrt(7x^2-19)))(x+2). $$

All! The uncertainty has disappeared. One more step and we come to the answer:

$$ -\frac(1)(6)\cdot \lim_(x\to 2)\frac((3x+1)(\sqrt(x^2+5)+\sqrt(7x^2-19)) )(x+2)=\\ =-\frac(1)(6)\cdot\frac((3\cdot 2+1)(\sqrt(2^2+5)+\sqrt(7\cdot 2 ^2-19)))(2+2)= -\frac(1)(6)\cdot\frac(7(3+3))(4)=-\frac(7)(4). $$

Answer: $\lim_(x\to 2)\frac(3x^2-5x-2)(\sqrt(x^2+5)-\sqrt(7x^2-19))=-\frac(7)( 4)$.

In the next example, consider the case where irrationalities will be present in both the numerator and the denominator of the fraction.

Example No. 3

Find $\lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9 ))$.

Since $\lim_(x\to 5)(\sqrt(x+4)-\sqrt(x^2-16))=\sqrt(9)-\sqrt(9)=0$ and $\lim_( x\to 5)(\sqrt(x^2-3x+6)-\sqrt(5x-9))=\sqrt(16)-\sqrt(16)=0$, then we have an uncertainty of the form $\frac (0)(0)$. Since in this case the roots are present in both the denominator and the numerator, in order to get rid of uncertainty you will have to multiply by two brackets at once. First, to the expression $\sqrt(x+4)+\sqrt(x^2-16)$ conjugate to the numerator. And secondly, to the expression $\sqrt(x^2-3x+6)-\sqrt(5x-9)$ conjugate to the denominator.

$$ \lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9 ))=\left|\frac(0)(0)\right|=\\ =\lim_(x\to 5)\frac((\sqrt(x+4)-\sqrt(x^2-16) )(\sqrt(x+4)+\sqrt(x^2-16))(\sqrt(x^2-3x+6)+\sqrt(5x-9)))((\sqrt(x^2 -3x+6)-\sqrt(5x-9))(\sqrt(x^2-3x+6)+\sqrt(5x-9))(\sqrt(x+4)+\sqrt(x^2 -16))) $$ $$ -x^2+x+20=0;\\ \begin(aligned) & D=1^2-4\cdot(-1)\cdot 20=81;\\ & x_1=\frac(-1-\sqrt(81))(-2)=\frac(-10)(-2)=5;\\ & x_2=\frac(-1+\sqrt(81))( -2)=\frac(8)(-2)=-4. \end(aligned) \\ -x^2+x+20=-1\cdot(x-5)(x-(-4))=-(x-5)(x+4). $$

For the expression $x^2-8x+15$ we get:

$$ x^2-8x+15=0;\\ \begin(aligned) & D=(-8)^2-4\cdot 1\cdot 15=4;\\ & x_1=\frac(-(- 8)-\sqrt(4))(2)=\frac(6)(2)=3;\\ & x_2=\frac(-(-8)+\sqrt(4))(2)=\frac (10)(2)=5. \end(aligned)\\ x^2+8x+15=1\cdot(x-3)(x-5)=(x-3)(x-5). $$

Substituting the resulting expansions $-x^2+x+20=-(x-5)(x+4)$ and $x^2+8x+15=(x-3)(x-5)$ into the limit under consideration, will have:

$$ \lim_(x\to 5)\frac((-x^2+x+20)(\sqrt(x^2-3x+6)+\sqrt(5x-9)))((x^2 -8x+15)(\sqrt(x+4)+\sqrt(x^2-16)))= \lim_(x\to 5)\frac(-(x-5)(x+4)(\ sqrt(x^2-3x+6)+\sqrt(5x-9)))((x-3)(x-5)(\sqrt(x+4)+\sqrt(x^2-16)) )=\\ =\lim_(x\to 5)\frac(-(x+4)(\sqrt(x^2-3x+6)+\sqrt(5x-9)))((x-3) (\sqrt(x+4)+\sqrt(x^2-16)))= \frac(-(5+4)(\sqrt(5^2-3\cdot 5+6)+\sqrt(5 \cdot 5-9)))((5-3)(\sqrt(5+4)+\sqrt(5^2-16)))=-6. $$

Answer: $\lim_(x\to 5)\frac(\sqrt(x+4)-\sqrt(x^2-16))(\sqrt(x^2-3x+6)-\sqrt(5x-9 ))=-6$.

In the next (second) part, we will consider a couple more examples in which the conjugate expression will have a different form than in the previous problems. The main thing to remember is that the purpose of using a conjugate expression is to get rid of the irrationality that causes uncertainty.

Liberation from irrationality in the denominator of a fraction

2015-06-13

Conjugate irrational expression

When transforming a fractional algebraic expression whose denominator contains an irrational expression, one usually tries to represent the fraction so that its denominator is rational. If $A, B, C, D, \cdots$ are some algebraic expressions, then you can specify rules with the help of which you can get rid of radical signs in the denominator of expressions of the form

$\frac(A)(\sqrt[n](B)), \frac(A)(B+C \sqrt(D)), \frac(A)(\sqrt(B) + c \sqrt(D )), \frac(A)( \sqrt(B) \pm \sqrt(C))$, etc.

1) To get rid of irrationality in the denominator of a fraction of the form $A/ \sqrt[n](B)$, multiply the numerator and denominator by $\sqrt[n](B^(n-1))$.
$\frac(A)(\sqrt[n](B)) = \frac(A \sqrt[n](B^(n-1)))(\sqrt[n](B) \sqrt[n] (B^(n-1))) = \frac(A \sqrt[n](B^(n-1)))(B)$.

Example 1. $\frac(4a^(2)b)(\sqrt(2ac)) = \frac(4a^(2)b \sqrt(4a^(2)c^(2)))(2ac) = \frac(2ab)(c) \sqrt(4a^(2)c^(2))$.

In the case of fractions of the form $\frac(A)(B+ C \sqrt(D)), \frac(A)(\sqrt(B) + c \sqrt(D))$ multiply the numerator and denominator by an irrational factor
$B – C \sqrt(D)$ or $\sqrt(B) – c \sqrt(D)$
respectively, i.e. to the conjugate irrational expression.

The meaning of the last action is that in the denominator the product of the sum and the difference is transformed into a difference of squares, which will already be a rational expression.

Example 2. Free yourself from irrationality in the denominator of the expression:
a) $\frac(xy)(\sqrt(x^(2) + y^(2)) + x)$; b) $\frac(2)(\sqrt(5) - \sqrt(3))$.

Solution, a) Multiply the numerator and denominator of the fraction by
expression $\sqrt(x^(2) + y^(2)) - x$. We get (provided that $y \neq 0$)
$\frac(xy)(\sqrt(x^(2) + y^(2)) + x) = \frac(xy (\sqrt(x^(2) + y^(2)) - x)) ((x^(2) + y^(2)) – x^(2)) = \frac(x)(y) (\sqrt(x^(2) + y^(2)) - x)$ ;
b) $\frac(2)(\sqrt(5) - \sqrt(3)) = \frac(2(\sqrt(5) + \sqrt(3)))(5 - 3) = \sqrt(5 ) + \sqrt(3)$.
3) In the case of expressions like
$\frac(A)(B \pm C \sqrt(D)), \frac(A)(\sqrt(B) \pm C \sqrt(D))$
the denominator is treated as the sum (difference) and multiplied by the partial square of the difference (sum) to obtain the sum (difference) of cubes. The numerator is also multiplied by the same factor.

Example 3. Free yourself from irrationality in the denominator of expressions:
a)$\frac(3)(\sqrt(5) + 1)$; b)$\frac(1)(\sqrt(a) – 2 \sqrt(b))$

Solution, a) Considering the denominator of this fraction as the sum of the numbers $\sqrt(5)$ and $1$, multiply the numerator and denominator by the partial square of the difference of these numbers:
$\frac(3)(\sqrt(5) + 1) = \frac(3 (\sqrt(5^(2)) - \sqrt(5) +1))((\sqrt(5) + 1) (\sqrt(5^(2)) - \sqrt(5) + 1)) = \frac(3(\sqrt(25) - \sqrt(5) + 1))((\sqrt(5))^ (3) +1)$,
or finally:
$\frac(3)(\sqrt(5) + 1) = \frac(3(\sqrt(25) - \sqrt(5) + 1))(6) = \frac(\sqrt(25) - \ sqrt(5) + 1)(2)$
b) $\frac(1)(\sqrt(a) – 2 \sqrt(b)) = \frac(\sqrt(a^(2)) + 2 \sqrt(ab) + 4 \sqrt(b^( 2)))((\sqrt(a))^(3) – (2 \sqrt(b))^(3)) = \frac( \sqrt(a^(2)) + 2 \sqrt(ab) + 4 \sqrt(b^(2)))(a-8b)$.

In some cases, it is necessary to perform a transformation of the opposite nature: to free the fraction from irrationality in the numerator. It is carried out in exactly the same way.

Example 4. Free yourself from irrationality in the numerator $\frac(\sqrt(a+b) - \sqrt(a-b))(2b)$.
Solution. $ \frac(\sqrt(a+b) - \sqrt(a-b))(2b) = \frac((a+b) – (a-b))(2b(\sqrt(a+b) + \sqrt(a-b ))) = \frac(1)(\sqrt(a+b) + \sqrt(a-b))$

Lesson No. 1 Lesson topic: “Liberation from irrationality in the denominator of a fraction”

Goals:

Educational:

Developmental:

Educational: fostering consistency in your actions.

Lesson type: learning new things

Lesson standard:

be able to find a way to get rid of irrationality

understand the meaning of “conjugate expression”

be able to get rid of irrationality in the denominator.

Equipment: cards for independent work.

During the classes

A little humor:

Do you know how to extract roots? - asks the teacher

Yes, sure. You need to pull the plant stem harder, and its root will be removed from the soil.

No, I meant another root, for example, from nine.

It will be “nine”, since “th” is a suffix.

I mean square root.

There are no square roots. They are fibrous and rod-like.

Arithmetic square root of nine.

That's what they would say! Square root of nine = 3!

Do you know how to extract roots?

2. “Repetition is the mother of learning.”

(8 min)

2.Checking the house/house№ 168 1)4; 2)10; 3)4;4) 8

3.Warm up. Follow the steps (Slide 1). Check in a circle counterclockwise.

1. Choose an unknown factor (Slide2)

Division into groups: according to selected figures.

Check in pairs of replacement composition.

They work individually and check, assessing points.

(Annex 1)

3. “A book is a book, but use your brains” (5 minutes)

(Slide 3) Two friends solved an equation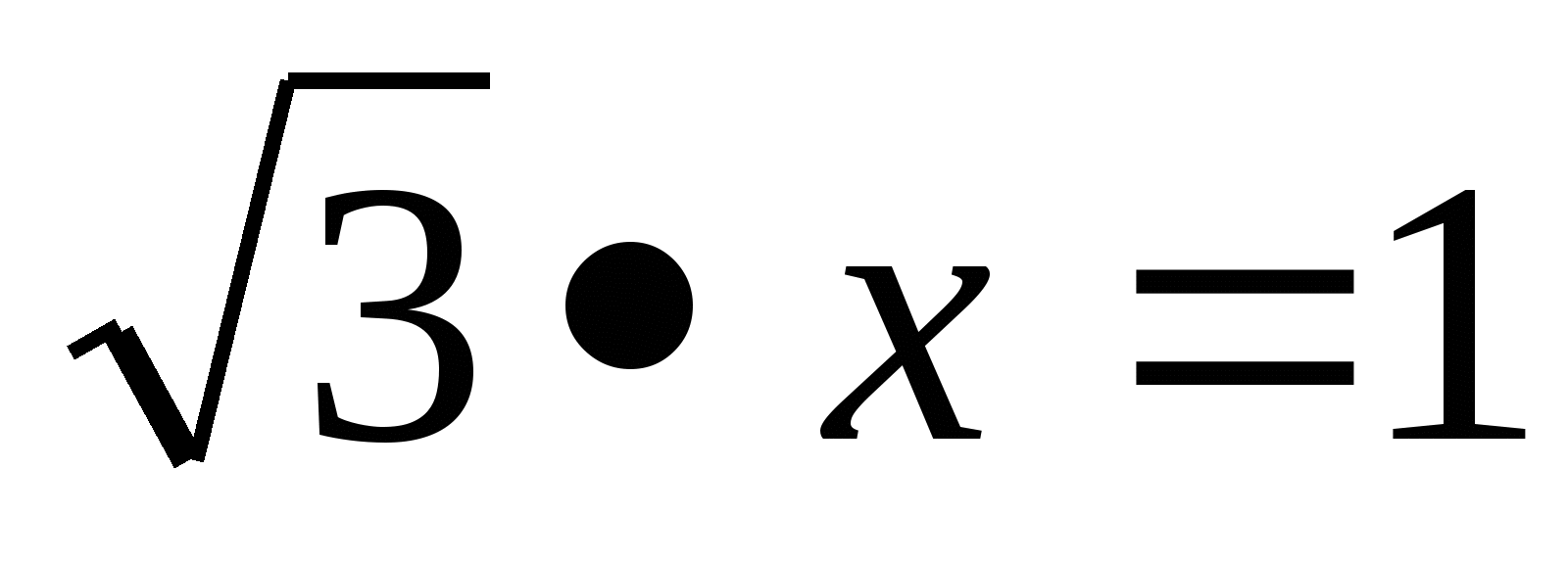
and received different answers. One of them picked x = , did a check. The second found the unknown factor by dividing the product by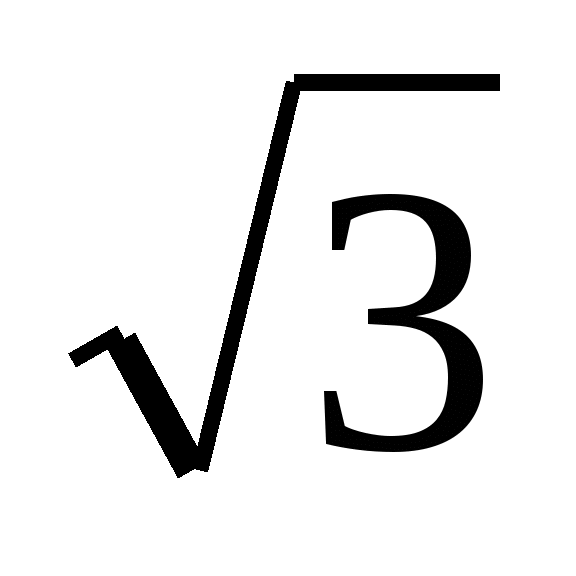
and got x = . Which one is right? Can a linear equation have two roots? The most convenient expression for calculations is one that does not contain irrationality in the denominator.

Lesson topic(Slide 4) : Liberation from irrationality in the denominator of a fraction

Goals(Slide 5) : become familiar with ways to get rid of irrationality in the denominators of a fraction. Developing the ability to free the denominator from irrationality;

Solve and check in pairs of shifts.

They discuss the situation and come to a conclusion.

Write down the topic

Formulate goals: become familiar with ways to get rid of irrationality in the denominators of a fraction.

developing the ability to determine the way to free yourself from irrationality;

4. Work on new material.

(10 min)

How to get rid of irrationality in the denominator? Do you want to know?

Working in groups on new material

Group performance

Pinning (Slide 6)

They work with a supporting outline. (Appendix 2)

Solve examples.

(Appendix 3)

Exchange information.

5. Charging (3 min)

Doing exercises

6. Independent work

(10 min)

By multi-level cards

1-in:

2-in:

3-in:

Perform individually, check by exchanging notebooks with another group.

The points are entered into the group's scorecard.

(Annex 1)

7.Creative task

(2 minutes)

Monkey - orange saleswoman (Slide 7)

Having once arrived at my dacha,

I found a problem there with the radicals.

She started throwing them all over the place.

We ask you, girls and boys,

Solve the problem on the monkey's tail.

Do you think we are done studying this topic? Let's continue in the next lesson.

They talk about what they will learn about this in the next lesson.

8. Homework: (2 minutes)

P.19 (Slide 7)

Level 1: No. 170 (1-6)

Level 2: No. 170 (1-6 and 9.12)

Creative task: Martyshkin’s task.

Write down

9. Lesson summary. Reflection

(3 min)

Two stars and a wish on stickers are attached to the selected emoticon (Slide 7)

The points are converted into a grade and a group scorecard is given to the teacher.

ANNEX 1

Group Scorecard.

0-8 points

Choose a multiplier

0-8 points

Working in a group on new material

0-5 points

Myself. Job

0-5 points

Lesson activity

0-5 points

APPENDIX 2

Supporting notes

If the denominator of an algebraic fraction contains a square root sign, then the denominator is said to contain irrationality. Transforming an expression to such a form that there are no square root signs in the denominator of the fraction is called liberation from irrationality in the denominator

There are several types irrationality fractions in the denominator. It is associated with the presence in it of an algebraic root of the same or different degrees. In order to get rid of irrationality, it is necessary to perform certain mathematical operations depending on the situation.

Instructions

1. Before getting rid of irrationality fractions in the denominator, its type should be determined, and depending on this, continue the solution. Indeed, any irrationality follows from the simple presence of roots; their different combinations and degrees are assumed by different algorithms.

2. Square root of the denominator, expression of the form a/?bEnter an additional factor equal to?b. In order for the fraction not to change, it is necessary to multiply both the numerator and the denominator: a/?b ? (a ?b)/b.Example 1: 10/?3 ? (10?3)/3.

3. Presence below the line fractions a root of a fractional power of the form m/n, and n>mThis expression looks like this: a/?(b^m/n).

4. Get rid of similar irrationality also by entering a multiplier, this time more difficult: b^(n-m)/n, i.e. from the exponent of the root itself, it is necessary to subtract the degree of the expression under its sign. Then only the first power will remain in the denominator: a/(b^m/n) ? a ?(b^(n-m)/n)/b. Example 2: 5/(4^3/5) ? 5 ?(4^2/5)/4 = 5 ?(16^1/5)/4.

5. Sum of square rootsMultiply both components fractions by a similar difference. Then, from the irrational addition of roots, the denominator is transformed into the difference of expressions/numbers under the root sign: a/(?b + ?c) ? a (?b – ?c)/(b – c).Example 3: 9/(?13 + ?23) ? 9 (?13 – ?23)/(13 – 23) = 9 (?23 – ?13)/10.

6. Sum/difference of cube rootsChoose as an additional factor the incomplete square of the difference if the denominator contains a sum, and, accordingly, the incomplete square of the sum for the difference of the roots: a/(?b ± ?c) ? a (?b? ? ?(b c) + ?c?)/ ((?b ± ?c) ?b? ? ?(b c) + ?c?) ?a (?b? ? ?(b c) + ? c?)/(b ± c).Example 4: 7/(?5 + ?4) ? 7 (?25-?20 +?16)/9.

7. If the problem contains both a square and a cube root, then divide the solution into two stages: stepwise derive the square root from the denominator, and then the cubic root. This is done according to the methods already known to you: in the first action you need to choose the multiplier of the difference/sum of the roots, in the second - the incomplete square of the sum/difference.

Tip 2: How to get rid of irrationality in the denominator

The correct notation for a fractional number does not contain irrationality V denominator. Such a notation is easier to understand in appearance, therefore, when irrationality V denominator It's smart to get rid of it. In this case, irrationality can become a numerator.

Instructions

1. To begin with, let's look at a primitive example - 1/sqrt(2). The square root of 2 is an irrational number in denominator.In this case, you need to multiply the numerator and denominator of the fraction by its denominator. This will provide a reasonable number in denominator. Indeed, sqrt(2)*sqrt(2) = sqrt(4) = 2. Multiplying 2 identical square roots by each other will result in what is under all of the roots: in this case, two. The result: 1/sqrt(2) = (1*sqrt(2))/(sqrt(2)*sqrt(2)) = sqrt(2)/2. This algorithm is also suitable for fractions, in denominator which the root is multiplied by a reasonable number. The numerator and denominator in this case must be multiplied by the root located in denominator.Example: 1/(2*sqrt(3)) = (1*sqrt(3))/(2*sqrt(3)*sqrt(3)) = sqrt(3)/(2*3) = sqrt( 3)/6.

2. Of course, something like this should be done if denominator It is not the square root that is found, but, say, the cubic root or any other degree. Root in denominator it is necessary to multiply by the same root, and the numerator is also multiplied by the same root. Then the root will go into the numerator.

3. In a more difficult case in denominator there is a sum or difference of an irrational and a reasonable number or 2 irrational numbers. In the case of the sum (difference) of 2 square roots or a square root and a reasonable number, you can use the famous formula (x+y)(x-y) = (x^2 )-(y^2). It will help you get rid of irrationality V denominator. If in denominator difference, then you need to multiply the numerator and denominator by the sum of the same numbers, if the sum - then by the difference. This multiplied sum or difference will be called conjugate to the expression in denominator.The result of this scheme is clearly visible in the example: 1/(sqrt(2)+1) = (sqrt(2)-1)/(sqrt(2)+1)(sqrt(2)-1) = (sqrt(2 )-1)/((sqrt(2)^2)-(1^2)) = (sqrt(2)-1)/(2-1) = sqrt(2)-1.

4. If in denominator there is a sum (difference) in which a root of a larger degree is present, then the situation becomes non-trivial and liberation from irrationality V denominator not invariably acceptable

Tip 3: How to free yourself from irrationality in the denominator of a fraction

A fraction consists of a numerator, located at the top of the line, and a denominator, the one it divides, located at the bottom. An irrational number is a number that cannot be represented in the form fractions with an integer in the numerator and a natural number in denominator. Such numbers are, say, the square root of 2 or pi. Traditionally, when talking about irrationality in denominator, the root is implied.

Instructions

1. Eliminate irrationality by multiplying by the denominator. This way the irrationality will be transferred to the numerator. When multiplying the numerator and denominator by the same number, the value fractions does not change. Use this option if each denominator is a root.

2. Multiply the numerator and denominator by the denominator the required number of times, depending on the root. If the root is square, then once.

3. Consider the square root example. Take the fraction (56-y)/√(x+2). It has a numerator (56-y) and an irrational denominator √(x+2), which is the square root.

4. Multiply the numerator and denominator fractions to the denominator, that is, to √(x+2). The original example (56-y)/√(x+2) will become ((56-y)*√(x+2))/(√(x+2)*√(x+2)). The result will be ((56-y)*√(x+2))/(x+2). Now the root is in the numerator, and in denominator there is no irrationality.

5. Not invariably the denominator fractions each one is under the root. Get rid of irrationality by using the formula (x+y)*(x-y)=x²-y².

6. Consider an example with the fraction (56-y)/(√(x+2)-√y). Its irrational denominator contains the difference of 2 square roots. Complete the denominator to form (x+y)*(x-y).

7. Multiply the denominator by the sum of the roots. Multiply the numerator by the same to get the value fractions hasn't changed. The fraction will take the form ((56-y)*(√(x+2)+√y))/((√(x+2)-√y)*(√(x+2)+√y)).

8. Take advantage of the above property (x+y)*(x-y)=x²-y² and free the denominator from irrationality. The result will be ((56-y)*(√(x+2)+√y))/(x+2-y). Now the root is in the numerator, and the denominator has gotten rid of irrationality.

9. In difficult cases, repeat both of these options, using as necessary. Note that it is not always possible to get rid of irrationality in denominator .

An algebraic fraction is an expression of the form A/B, where the letters A and B stand for any number or letter expressions. Often the numerator and denominator in algebraic fractions have a massive form, but operations with such fractions should be done according to the same rules as actions with ordinary ones, where the numerator and denominator are positive integers.

Instructions

1. If given mixed fractions, convert them to irregular fractions (a fraction in which the numerator is larger than the denominator): multiply the denominator by the whole part and add the numerator. So the number 2 1/3 will turn into 7/3. To do this, multiply 3 by 2 and add one.

2. If you need to convert a decimal to an improper fraction, think of it as dividing a number without a decimal point by one with as many zeros as there are numbers after the decimal point. Let's say, imagine the number 2.5 as 25/10 (if you shorten it, you get 5/2), and the number 3.61 - as 361/100. Operating with improper fractions is often easier than with mixed or decimal fractions.

3. If fractions have identical denominators and you need to add them, then simply add the numerators; the denominators remain unchanged.

4. If you need to subtract fractions with identical denominators, subtract the numerator of the 2nd fraction from the numerator of the first fraction. The denominators also do not change.

5. If you need to add fractions or subtract one fraction from another, and they have different denominators, reduce the fractions to a common denominator. To do this, find a number that will be the least universal multiple (LCM) of both denominators or several if the fractions are larger than 2. LCM is a number that will be divided into the denominators of all given fractions. For example, for 2 and 5 this number is 10.

6. After the equal sign, draw a horizontal line and write this number (NOC) into the denominator. Add additional factors to the entire term - the number by which you need to multiply both the numerator and the denominator in order to get the LCM. Multiply the numerators step by step by additional factors, preserving the sign of addition or subtraction.

7. Calculate the total, reduce it if necessary, or select the entire part. For example, do you need to fold it? And?. The LCM for both fractions is 12. Then the additional factor for the first fraction is 4, for the 2nd fraction - 3. Total: ?+?=(1·4+1·3)/12=7/12.

8. If an example is given for multiplication, multiply the numerators together (this will be the numerator of the total) and the denominators (this will be the denominator of the total). In this case, there is no need to reduce them to a common denominator.

9. To divide a fraction by a fraction, you need to turn the second fraction upside down and multiply the fractions. That is, a/b: c/d = a/b · d/c.

10. Factor the numerator and denominator as needed. For example, move the universal factor out of the bracket or expand it according to abbreviated multiplication formulas, so that after this you can, if necessary, reduce the numerator and denominator by GCD - the minimum universal divisor.

Note!
Add numbers with numbers, letters of the same kind with letters of the same kind. Let's say it is impossible to add 3a and 4b, which means that their sum or difference will remain in the numerator - 3a±4b.

In everyday life, fake numbers are more common: 1, 2, 3, 4, etc. (5 kg of potatoes), and fractional, non-integer numbers (5.4 kg of onions). Many of them are presented in form decimal fractions. But represent the decimal fraction in form fractions pretty easy.

Instructions

1. Let's say the number “0.12” is given. If you do not reduce this decimal fraction and present it as it is, then it will look like this: 12/100 (“twelve hundredths”). In order to get rid of a hundred in the denominator, you need to divide both the numerator and the denominator by a number that divides them into integers. This number is 4. Then, dividing the numerator and denominator, we get the number: 3/25.

2. If we look more at everyday life, we can often see on the price tag of products that its weight is, for example, 0.478 kg or so on. This number is also easy to imagine in form fractions:478/1000 = 239/500. This fraction is quite ugly, and if there was a probability, then this decimal fraction would be allowed to be reduced further. And all in the same way: selecting a number that divides both the numerator and the denominator. This number is called the greatest universal factor. The factor is named “largest” because it is much more convenient to immediately divide both the numerator and the denominator by 4 (as in the first example) than to divide it twice by 2.

Video on the topic

Decimal fraction– variety fractions, which has a “round” number in the denominator: 10, 100, 1000, etc., Say, fraction 5/10 has a decimal notation of 0.5. Based on this thesis, fraction can be represented as a decimal fractions .

Instructions

1. Possible, need to be represented as a decimal fraction 18/25. First, you need to make sure that one of the “round” numbers appears in the denominator: 100, 1000, etc. To do this, you need to multiply the denominator by 4. But you will need to multiply both the numerator and the denominator by 4.

2. Multiplying the numerator and denominator fractions 18/25 by 4, it turns out 72/100. This is recorded fraction in decimal form: 0.72.

When dividing 2 decimal fractions, when there is no calculator at hand, many experience some difficulties. There's really nothing difficult here. Decimal fractions are called such if their denominator has a number that is a multiple of 10. As usual, such numbers are written on one line and have a comma separating the fractional part from the whole. Apparently due to the presence of a fractional part, which also differs in the number of digits after the decimal point, it is not clear to many how to perform mathematical operations with such numbers without a calculator.

You will need

sheet of paper, pencil

Instructions

1. It turns out that in order to divide one decimal fraction by another, you need to look at both numbers and determine which of them has more digits after the decimal point. We multiply both numbers by a number that is a multiple of 10, i.e. 10, 1000 or 100000, the number of zeros in which is equal to the greater number of digits after the decimal point of one of our 2 initial numbers. Now both are decimal fractions turned into ordinary integers. Take a sheet of paper with a pencil and separate the two resulting numbers with a “corner”. We get the result.

2. Let's say we need to divide the number 7.456 by 0.43. The first number has more decimal places (3 decimal places), therefore we multiply both numbers not by 1000 and get two primitive integers: 7456 and 430. Now we divide 7456 by 430 with a “corner” and we get that if 7.456 is divided by 0.43 it will come out approximately 17.3.

3. There is another division method. Writing down decimals fractions in the form of primitive fractions with a numerator and denominator, for our case these are 7456/1000 and 43/100. Later, we write down the expression for dividing 2 primitive fractions: 7456*100/1000*43, after that we reduce the tens, we get: 7456/10*43 = 7456/430 In the final output we again get the division of 2 primitive numbers 7456 and 430, which can be produced with a “corner”.

Video on the topic

Helpful advice
Thus, the way to divide decimal fractions is to reduce them to whole numbers, with the support of multiplying each of them by the same number. Performing operations with integers, as usual, does not cause any difficulties for anyone.

Video on the topic