“Y = tgx, y = ctgx funksiyaları, onların xassələri və qrafikləri” dərsi. “Y = tgx, y = ctgx funksiyaları, onların xassələri və qrafikləri” dərsi Tangensi olan funksiyaların tədqiqi.
Bu video dərslik funksiyaların xassələrini müzakirə edir y =tgx, y = ctgx, onların qrafiklərinin necə qurulacağını göstərir.
Video dərslik funksiyaya nəzər salmaqla başlayır y =tgx.
Funksiyanın xassələri vurğulanır.
1) Funksiya sahəsi y =tgx istisna olmaqla, bütün real ədədlər çağırılır x =π/2 + 2 πk. Bunlar. qrafikdə xəttə aid olan nöqtələr yoxdur x =π/2 və x = -π/2, eləcə də x = 3π/2 və s (eyni dövriliklə). Beləliklə, funksiyanın qrafiki y =tgx düz xətlər arasındakı boşluqlarda yerləşəcək sonsuz sayda budaqlardan ibarət olacaqdır x = - 3π/2 və x = -π/2, x = -π/2 və x = π/2 və s.
2) Funksiya y =tgx periyodikdir, burada əsas dövr π-dir. Bu bərabərliyi təsdiqləyir tg(x- π ) = tg x =tg(x+π ) . Bu bərabərliklər əvvəllər öyrənilmişdi, müəllif hər hansı etibarlı dəyər üçün tələbələri onları xatırlamağa dəvət edir. t bərabərliklər etibarlıdır:
tg(t+ π ) = tg t, və c tg(t+π ) = ctg t. Bu bərabərliklərin nəticəsi odur ki, əgər y = tan funksiyasının qrafikinin bir qolu x xətlər arasında X = - π/2 və X= π/2, onda qalan budaqlar bu budağı x oxu boyunca sürüşdürməklə əldə edilə bilər. π, 2π və s.
3) Funksiya y =tgx qəribədir, çünki . tg(- x) =- tg x.
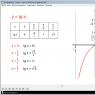
Sonra funksiyanın qrafikinin qurulmasına keçək y =tgx. Yuxarıda təsvir edilən funksiyanın xassələrindən aşağıdakı kimi, funksiya y =tgx dövri və tək. Buna görə də, qrafikin bir hissəsini - bir intervalda bir filial qurmaq və sonra köçürmə üçün simmetriyadan istifadə etmək kifayətdir. Müəllif dəyərlərin hesablandığı bir cədvəl təqdim edir tgx müəyyən dəyərlərdə x daha dəqiq plan qurmaq üçün. Bu nöqtələr koordinat oxunda qeyd olunur və hamar bir xətt ilə birləşdirilir. Çünki Qrafik koordinatların mənşəyinə görə simmetrik olarsa, koordinatların mənşəyinə görə simmetrik olaraq eyni budaq qurulur. Nəticədə qrafikin bir qolunu alırıq y =tgx. Sonra, x oxu boyunca π, 2 π və s. ilə sürüşmədən istifadə edərək qrafik əldə edilir. y =tgx.
Funksiya qrafiki y =tgx tangentoid adlanır və şəkildə göstərilən qrafikin üç qolu tangentoidin əsas qollarıdır.
4) Funksiya y =tgx intervalların hər birində (- + ; +) artır.
5) Funksiya qrafiki y =tgx yuxarıda və aşağıda heç bir məhdudiyyət yoxdur.
6) Funksiya y =tgxən böyük və ən kiçik dəyəri yoxdur.
7) Funksiya y =tgx istənilən intervalda davamlı (- - π/2+π;π/2+π). π/2+π düz xətti funksiyanın qrafikinin asimptotu adlanır y =tgx, çünki bu nöqtələrdə funksiyanın qrafiki kəsilir.
8) Funksiya qiymətlərinin çoxluğu y =tgx bütün həqiqi ədədlər çağırılır.
Daha sonra video dərsində bir nümunə verilir: ilə tənliyi həll edin tgx. Həll etmək üçün funksiyanın 2 qrafikini quracağıq saat və bu qrafiklərin kəsişmə nöqtələrini tapın: bu, absisləri πk ilə fərqlənən sonsuz nöqtələr toplusudur. Bu tənliyin kökü olacaq X= π/6 +πk.
Funksiyanın qrafikini nəzərdən keçirək y =ctgx. Bir funksiyanın qrafiki iki şəkildə çəkilə bilər.
Birinci üsul, qrafikin qurulmasına bənzər bir qrafikin qurulmasını əhatə edir y = funksiyalarıtgx. Funksiya qrafikinin bir qolunu quraq y = ctgx xətlər arasında X= 0u X= π. Sonra simmetriya və dövrilikdən istifadə edərək qrafikin digər qollarını quracağıq.
İkinci üsul daha sadədir. Funksiya qrafiki y = сtgx reduksiya düsturundan istifadə edərək tangensləri çevirməklə əldə edilə bilər ilətgx = - tg(x +π/2). Bunun üçün funksiya qrafikinin bir qolunu dəyişdirək y = tgx x oxu boyunca π/2 sağa. Qalan budaqlar bu budağı x oxu boyunca π, 2π və s.-ə sürüşdürməklə əldə edilir. y = ctg funksiyasının qrafiki x tangentoid də adlanır və qrafikin (0;π) intervalında qolu tangenoidin əsas qoludur.
MƏTNİN KOD EDİLMƏSİ:
y = tan x (y tangens x-ə bərabərdir), y = ctg x (y kotangens x-ə bərabərdir) funksiyasının xassələrini nəzərdən keçirəcəyik və onların qrafiklərini quracağıq. y = tgx funksiyasını nəzərdən keçirək

y = tan x funksiyasının qrafikini çəkməzdən əvvəl bu funksiyanın xassələrini yazaq.
XÜSUSİYYƏT 1. y = tan x funksiyasının təyin olunma oblastı x = + πk formalı ədədlər istisna olmaqla, bütün həqiqi ədədlərdir (x iki üzərində pi və pi ka cəminə bərabərdir).
Bu o deməkdir ki, bu funksiyanın qrafikində x = xəttinə (k = 0 ka sıfıra bərabər olarsa alırıq) və x = xəttinə (x mənfi pi ikiyə bərabərdir) aid olan nöqtələr yoxdur (biz almaq əgər k = - 1 ka mənfi birə bərabərdir), və düz xətti x = (x üç pi ikiyə bərabərdir) (k = 1 birə bərabər olarsa əldə edirik) və s. Bu o deməkdir ki, qrafik y = tan x funksiyasının düz xətlər arasındakı intervallarda yerləşəcək sonsuz sayda budaqlardan ibarət olacaqdır. Məhz, x = və x arasındakı bandda =-; zolaqda x = - və x = ; zolaqda x = və x = və s. sonsuz olaraq.
XALQ 2. y = tan x funksiyası əsas dövr π ilə dövridir. (Çünki ikiqat bərabərlik doğrudur
tan(x- π) = tanx = tan (x+π) x minus pi tangensi x-in tangensine və x plus pi-nin tangensinə bərabərdir). Tangens və kotangensi öyrənərkən bu bərabərliyi nəzərə aldıq. Onu xatırladaq:
t-nin hər hansı icazə verilən dəyəri üçün bərabərliklər etibarlıdır:
tg (t + π)= tgt
ctg (t + π) = ctgt
Bu bərabərlikdən belə nəticə çıxır ki, y = tan x funksiyasının qrafikinin x = - və x = intervalında budaqını quraraq, qurulmuş budağı X oxu boyunca π, 2π ilə sürüşdürərək qalan budaqları əldə edirik. , və s.
XÜSUSİYYƏT 3. tg (- x) = - tan x bərabərliyi doğru olduğu üçün y = tan x funksiyası tək funksiyadır.
y = tan x funksiyasının qrafikini çəkək
Bu funksiya dövri olduğundan, sonsuz sayda budaqlardan (x = və x = arasındakı zolaqda, həmçinin x = və x = arasındakı zolaqda və s.) və tək olduğundan, biz budaqların bir hissəsini quracağıq. sıfırdan pi-yə qədər olan intervalda nöqtə-nöqtə iki (), sonra mənşə və dövriliyin simmetriyasından istifadə edin.
Planlaşdırma üçün tangens dəyərlər cədvəlini quraq.
Birinci nöqtəni tapırıq: x = 0 tan x = 0-da (x sıfıra bərabərdir, tan x də sıfıra bərabərdir); növbəti nöqtə: at x = tan x = (x piyə altıya bərabərdir, x tangensi üçə üçə bərabərdir); Aşağıdakı məqamları qeyd edək: x = tan x = 1-də (x dörd tən piyə bərabərdir x birə bərabərdir) və x = tg x = (x pi-yə üç tan x kvadrat kökə bərabərdir) üçdən). Yaranan nöqtələri koordinat müstəvisində qeyd edin və onları hamar bir xətt ilə birləşdirin (şəkil 2).
Funksiyanın qrafiki koordinatların mənşəyinə görə simmetrik olduğundan, eyni budaqı koordinatların başlanğıcına görə simmetrik şəkildə quracağıq. (şək. 3).
Və nəhayət, dövriliyi tətbiq edərək, y = tan x funksiyasının qrafikini alırıq.
y = tan x funksiyasının qrafikinin x = - və x = olan zolağında qolunu qurmuşuq. Qalan budaqları, qurulmuş budağı X oxu boyunca π, 2π və s. ilə sürüşdürərək qururuq.

Yaradılan süjetə tangentoid deyilir.
Şəkil 3-də göstərilən tangentoid hissəsi tangentoidin əsas qolu adlanır.
Qrafikə əsaslanaraq bu funksiyanın daha bir neçə xassələrini yazacağıq.
XÜSUSİYYƏT 4. y = tan x funksiyası intervalların hər birində artır (mənfi pi-dən iki üstəgəl pi ka-dan pi-yə iki üstəgəl pi ka).
XÜSUSİYYƏT 5. y = tan x funksiyası nə yuxarıda, nə də aşağıda məhdudlaşmır.
XÜSUSİYYƏT 6. y = tan x funksiyasının nə böyük, nə də ən kiçik qiymətləri var.
XÜSUSİYYƏT 7. y = tan x funksiyası formanın istənilən intervalında fasiləsizdir (mənfi pi-dən iki üstəgəl pi ka-dan pi-yə iki üstəgəl pi ka).
x = + πk formalı düz xətt (x iki və pi ka üzərində pi cəminə bərabərdir) funksiyanın qrafikinin şaquli asimptotudur, çünki x = + πk formasının nöqtələrində funksiya a təsir göstərir. fasiləsizlik.
XÜSUSİYYƏT 8. y = tan x funksiyasının qiymətlər çoxluğu bütün həqiqi ədədlərdir, yəni (eff-dən eff mənfi sonsuzluqdan üstəgəl sonsuzluğa qədər olan intervala bərabərdir).
NÜMUNƏ 1. tg x = tənliyini həll edin (tangens x üçə üçün kökünə bərabərdir).
Həll. Bir koordinat sistemində y = tan x funksiyalarının qrafiklərini quraq
(y x-ın tangensinə bərabərdir) və y = (y üçə bölünən üçün kökünə bərabərdir).
Absisləri bir-birindən πk (pi ka) ilə fərqlənən sonsuz sayda kəsişmə nöqtələri əldə etdik.tg x = x = nöqtəsində olduğundan, əsas budaqda kəsişmə nöqtəsinin absisi (pi altı ilə) bərabərdir.
Bu tənliyin bütün həllərini x = + πk düsturu ilə yazırıq (x pi çarpı altı üstəgəl pi ka).
Cavab: x = + πk.
y = сtg x funksiyasının qrafikini quraq.
İki tikinti üsulunu nəzərdən keçirək.
Birinci yol y = tan x funksiyasının qrafikinə bənzəyir.
Bu funksiya dövri olduğundan, sonsuz sayda budaqlardan (x = 0 ilə x =π arasındakı zolaqda, həmçinin x =π ilə x = 2π arasındakı zolaqda və s.) və tək olduğundan, biz quracağıq. qrafikin bir hissəsi sıfırdan pi-yə qədər olan intervalda iki (), onda simmetriya və dövrilikdən istifadə edəcəyik.
Qrafik qurmaq üçün kotangent dəyərlər cədvəlindən istifadə edək.
Yaranan nöqtələri koordinat müstəvisində qeyd edin və onları hamar bir xətt ilə birləşdirin.
Funksiya qrafiki nisbətən simmetrik olduğundan, eyni budaqı simmetrik şəkildə quracağıq.
Dövriliyi tətbiq edək və y = сtg x funksiyasının qrafikini alaq.
y = сtg x funksiyasının qrafikinin x = 0 və x =π-dən olan zolağında qolunu qurmuşuq. Qalan budaqları x oxu boyunca π, - π, 2π, - 2π və s. ilə sürüşdürərək qururuq.
İkinci yol y =сtg x funksiyasının qrafikini çəkmək.
y =сtg x funksiyasının qrafikini əldə etməyin ən asan yolu reduksiya düsturundan istifadə edərək tangensi çevirməkdir (x kotangenti x və pi cəminin tangensini ikiyə bərabərdir).

Bu zaman ilk olaraq y =tg x funksiyasının qrafikinin budağını absis oxu boyunca sağa sürüşdürürük, alırıq.
y = tg (x+), sonra isə yaranan qrafikin absis oxuna nisbətən simmetriyasını yerinə yetiririk. Nəticə y =сtg x funksiyasının qrafikinin budağı olacaq (şək. 4). Bir filialı bilməklə, funksiyanın dövriliyindən istifadə edərək bütün qrafiki qura bilərik. Qalan budaqları, qurulmuş budağı x oxu boyunca π, 2π və s. dəyişdirərək qururuq.
y =сtg x funksiyasının qrafiki də y =tg x funksiyasının qrafiki kimi tangentoid adlanır. Sıfırdan piyə qədər intervalda yerləşən budaq y = сtg x funksiyasının qrafikinin əsas budağı adlanır.
A nöqtəsində mərkəzləşdirilmişdir.
α radyanla ifadə olunan bucaqdır.
Tangens ( tan α) düzbucaqlı üçbucağın hipotenuzası ilə ayağı arasındakı α bucağından asılı olaraq qarşı tərəfin uzunluğunun nisbətinə bərabər olan triqonometrik funksiyadır |BC| bitişik ayağın uzunluğuna |AB| .
kotangent ( ctg α) düzbucaqlı üçbucağın hipotenuzası ilə ayağı arasındakı α bucağından asılı olaraq bitişik ayağın uzunluğunun nisbətinə bərabər olan triqonometrik funksiyadır |AB| qarşı ayağın uzunluğuna |BC| .
Tangens
Harada n- bütöv.
Qərb ədəbiyyatında tangens aşağıdakı kimi qeyd olunur:
.
;
;
.
Tangens funksiyasının qrafiki, y = tan x
Kotangent
Harada n- bütöv.
Qərb ədəbiyyatında kotangens aşağıdakı kimi işarələnir:
.
Aşağıdakı qeydlər də qəbul edilir:
;
;
.
Kotangens funksiyasının qrafiki, y = ctg x

Tangens və kotangensin xassələri
Dövrilik
Funksiyalar y = tg x və y = ctg xπ dövrü ilə dövri olur.
Paritet
Tangens və kotangens funksiyaları təkdir.
Tərif sahələri və dəyərlər, artan, azalan
Tangens və kotangens funksiyaları öz təyinat sahəsində davamlıdır (davamlılığın sübutuna baxın). Tangens və kotangensin əsas xüsusiyyətləri cədvəldə verilmişdir ( n- bütöv).
| y = tg x | y = ctg x | |
| Əhatə dairəsi və davamlılıq | ||
| Dəyərlər diapazonu | -∞ < y < +∞ | -∞ < y < +∞ |
| Artan | - | |
| Azalan | - | |
| İfrat | - | - |
| Sıfırlar, y = 0 | ||
| Ordinat oxu ilə kəsişən nöqtələr, x = 0 | y = 0 | - |
Formulalar
Sinus və kosinusdan istifadə edən ifadələr
;
;
;
;
;
Cəm və fərqdən tangens və kotangens üçün düsturlar
Qalan düsturları, məsələn, əldə etmək asandır
Tangenslərin məhsulu
Tangenslərin cəmi və fərqi üçün düstur
Bu cədvəl arqumentin müəyyən dəyərləri üçün tangens və kotangentlərin dəyərlərini təqdim edir. 
Kompleks ədədlərdən istifadə edən ifadələr
Hiperbolik funksiyalar vasitəsilə ifadələr
;
;
Törəmələri
; .
.
Funksiyanın x dəyişəninə münasibətdə n-ci dərəcəli törəmə:
.
Tangens üçün düsturların alınması > > > ; kotangens üçün > > >
İnteqrallar
Serialın genişləndirilməsi
X-in güclərində tangensin genişlənməsini əldə etmək üçün funksiyalar üçün güc seriyasında genişlənmənin bir neçə şərtini götürməlisiniz. günah x Və cos x və bu çoxhədliləri bir-birinə bölmək, . Bu, aşağıdakı düsturları yaradır.
.
at.
Harada Bn- Bernoulli nömrələri. Onlar ya təkrarlanma əlaqəsindən müəyyən edilir:
;
;
Harada.
Və ya Laplas düsturuna görə: 
Tərs funksiyalar
Tangens və kotangensin tərs funksiyaları müvafiq olaraq arktangens və arktangensdir.
Arktangens, arctg
, Harada n- bütöv.
Arkkotangent, arkctg
, Harada n- bütöv.
İstinadlar:
İ.N. Bronstein, K.A. Semendyaev, Mühəndislər və kollec tələbələri üçün riyaziyyat kitabçası, "Lan", 2009.
G. Korn, Alimlər və Mühəndislər üçün Riyaziyyat Kitabı, 2012.
, [−5π/2; −3π/2],. . . - bir sözlə, bütün seqmentlər üzrə [−π/2 + 2πk; π/2 + 2πk], burada k Z və bütün seqmentlərdə azalır
[π/2 + 2πn; 3π/2 + 2πn], burada n Z.
Məsələ 11.6. y = cos x funksiyası hansı seqmentlərdə artır, hansı seqmentlərdə azalır?
Problem 11.8. Artan ardıcıllıqla düzün: sin 1, cos 2, sin 3, cos 4, sin 5, cos 6.
§ 12. Tangens və kotangensin qrafikləri
y = tan x funksiyasının qrafikini çəkək. Əvvəlcə onu (−π/2; π/2) intervalına aid olan x ədədləri üçün quraq.
Əgər x = 0 olarsa, onda tan x = 0; x 0-dan π/2-yə qədər artdıqda tan x də artır - bu, tangens oxuna baxdıqda görünə bilər (şək. 12.1 a). x π/2-yə yaxınlaşdıqca daha kiçik qalır

düyü. 12.2. y = tan x.
π/2, tan x-in dəyəri artır (şəkil 12.1 a-da M nöqtəsi daha yüksək və daha yüksək olur) və açıq-aydın, özbaşına böyük müsbət ədədə çevrilə bilər. Eyni şəkildə, x 0-dan −π/2-yə qədər azaldıqca tan x mənfi ədədə çevrilir, onun mütləq qiyməti x −π/2-yə yaxınlaşdıqca artır. x = π/2 və ya −π/2 üçün tan x funksiyası qeyri-müəyyəndir. Buna görə də x (−π/2; π/2) üçün y = tan x qrafiki təqribən şəkildəki kimi görünür. 12.1 b.
Koordinatların mənşəyinin yaxınlığında əyrimiz y = x x düz xəttinə yaxındır: axı, kiçik iti bucaqlar üçün tg x ≈ x təxmini bərabərliyi doğrudur. Deyə bilərik ki, y = x xətti başlanğıcda y = tan x funksiyasının qrafikinə toxunur. Bundan əlavə, 12.1 b-dəki əyri mənşəyə görə simmetrikdir. Bu onunla izah olunur ki, y = tan x funksiyası təkdir, yəni tg(−x) = − tan x eyniliyini saxlayır.
Bütün x üçün y = tan x funksiyasının qrafikini çəkmək üçün xatırlayaq ki, tan x π dövrü ilə dövri funksiyadır. Buna görə də y = tan x funksiyasının tam qrafikini əldə etmək üçün şəkildəki əyrini sonsuz dəfələrlə təkrarlamaq lazımdır. 12.1 b, onu absis boyunca πn məsafələrinə köçürün, burada n tam ədəddir. y = tan x funksiyasının qrafikinin yekun görünüşü Şek. 12.2.
Qrafikə əsasən bir daha görürük ki, y = tan x funksiyası

düyü. 12.3. y = cotg x.
x = π/2 + πn, n Z, yəni cos x = 0 olan x üçün müəyyən edilmir. x = π/2, 3π/2, tənlikləri olan şaquli xətlər. . . , qrafın yaxınlaşdığı budaqlar qrafikin asimptotları adlanır.
Eyni əncirdə. 12.2 tg x = a tənliyinin həllərini təsvir etdik.
y = çarpayı x funksiyasının qrafikini çəkək. Ən asan yol ctg x = tan(π/2 − x) reduksiya düsturundan istifadə edərək əvvəlki paraqrafda təsvir etdiyimizə oxşar çevrilmələrdən istifadə edərək y = tan x funksiyasının qrafikindən bu qrafiki əldə etməkdir. Nəticə Şəkildə göstərilmişdir. 12.3
Problem 12.1. y = ctg x funksiyasının qrafiki müəyyən xətt ətrafında simmetriyadan istifadə etməklə y = tan x funksiyasının qrafikindən alınır. Hansı? Bu əmlakla başqa xətlər varmı?
Problem 12.2. Koordinatları (π/2; 0) olan nöqtədə y = cot x funksiyasının qrafikinə toxunan düz xəttin tənliyi necə görünür?
Problem 12.3. Rəqəmləri müqayisə edin: a) tg(13π/11) və tg 3.3π; b) tan 9,6π və ctg(−11,3π).

Problem 12.4. Rəqəmləri artan ardıcıllıqla düzün: tg 1, tg 2, tg 3, tg 4, tg 5.
Məsələ 12.5. Funksiyaların qrafiki:
a) y = tan(2x − π/3); |
b) y = 2 çarpayı (π/4 − x). |
Problem 12.6. Funksiyaların qrafiki: |
|
a) y = arktan x; |
b) y = arcctg x. |
Problem 12.7. y = arctan x + arctan(1/x) funksiyasının qrafikini çəkin.
§ 13. sin x + cos x nəyə bərabərdir?
Bu bölmədə biz aşağıdakı məsələni həll etməyə çalışacağıq: sin x + cos x ifadəsinin ala biləcəyi ən böyük qiymət nədir?
Əgər düzgün saymısınızsa, bu cədvələ daxil edilmiş bütün x-lərin ən böyük dəyərinin sin x + cos x olduğunu tapmalı idiniz.
x üçün 45◦-ə yaxın və ya radian ölçüsü ilə π/4-ə yaxın alınır.
Əgər x = π/4 olarsa, sin x+cos x-in dəqiq qiyməti 2-dir. Məlum olur ki, bizim nəticəmiz eksperimental olaraq və
əslində doğrudur: bütün x üçün sin x + cos x 6 bərabərsizliyi doğrudur
2, buna görə də 2 bu ifadə ilə qəbul edilən ən böyük qiymətdir.
Bu bərabərsizliyi ən təbii şəkildə sübut etmək üçün hələ kifayət qədər imkanlarımız yoxdur. Hələlik onu planimetriya probleminə necə endirəcəyimizi göstərəcəyik.
Əgər 0< x < π/2, то sin x и cos x - катеты прямоугольного треугольника с гипотенузой 1 и острым углом x (рис. 13.1 ).
Buna görə də, vəzifəmiz aşağıdakı kimi yenidən qurulur: hipotenuzası 1 olan düzbucaqlı üçbucağın ayaqlarının uzunluqlarının cəminin bu üçbucaq ikitərəfli olarsa maksimum olacağını sübut etmək.
Problem 13.1. Bu ifadəni sübut edin.
Hi- ilə ikitərəfli düzbucaqlı olduğundan
Potenuza 1, ayaqların uzunluqlarının cəmi 2√-ə bərabərdir, bu məsələnin nəticəsi (0; π/2) intervalında yatan bütün x üçün sin x + cos x 6 2 bərabərsizliyini nəzərdə tutur. Buradan belə nəticəyə gəlmək çətin deyil ki, bu bərabərsizlik ümumilikdə bütün x üçün keçərlidir.
Məsələ 13.1-in nəticəsi təkcə düzbucaqlı üçbucaqlar üçün deyil.
Məsələ 13.2. AC tərəfinin və B bucağının verilmiş qiymətləri olan bütün üçbucaqlar arasında ən böyük AB + BC cəminin AC əsası olan ikitərəfli üçbucaq üçün olacağını sübut edin.
Gəlin triqonometriyaya qayıdaq.
Məsələ 13.3. § 3-dən sinuslar cədvəlindən istifadə edərək y = sin x + cos x funksiyasının nöqtəli qrafikini qurun.
Qeyd. Unutmayın ki, x radyanla ifadə edilməlidir; İntervaldan kənar x dəyərləri üçün azalma düsturlarından istifadə edin.
Hər şeyi düzgün etmisinizsə, sinus dalğasına bənzəyən bir əyriniz olmalıdır. Daha sonra görəcəyik ki, bu əyri sadəcə oxşar deyil, sinusoiddir. Biz həmçinin 3 sin x + 4 cos x kimi ifadələrin ən böyük qiymətlərini tapmağı öyrənəcəyik (yeri gəlmişkən, y = 3 sin x + 4 cos x funksiyasının qrafiki də sinusoiddir!).